搜索
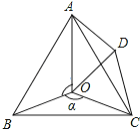
【题目】如图，点
是等边
内一点，
，
．以
为一边作等边三角形
，连接
、
．
（1）若
，判断
_______
(填“
，
或
”)
（2）当
，试判断
的形状，并说明理由；
（3）探究：当
______时，是等腰三角形．(请直接写出答案)
参考答案：
【答案】（1）=；（2）
是直角三角形，证明见详解；（3）
、
、
．
【解析】
（1）根据等边三角形性质得出
，利用
求出
，所以B，O，D三点共线，即有
；
（2）首先根据已知条件可以证明
，然后利用全等三角形的性质可以求出
的度数，由此即可判定
的形状；
（3）分三种情况讨论，利用已知条件及等腰三角形的性质即可求解．
解：（1）答：
证明∵
是等边三角形，
∴，
当
，即时，
，
即：B，O，D三点共线，
∴
（2）是直角三角形．
是等边三角形，
，
是等边三角形，
，
，
，
，
，
，
，
，
是直角三角形；
（3）由（2）知，
∴
，
∴
，
，
，
①要使
，需
，
，
；
②要使
，需
，
，
；
③要使
，需
，
，
．
所以，当
为、、时，是等腰三角形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】探究：如图①，在△ABC 中，∠BAC＝90°，AB＝AC，直线 m 经过点 A，BD⊥m 于点 D，CE⊥m 于点 E，求证：△ABD≌△CAE．
应用：如图②，在△ABC 中，AB＝AC，D、A、E 三点都在直线 m 上，并且有∠BDA＝∠AEC＝∠BAC，求证：DE＝BD+CE．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图 1，是一个长为 2m，宽为 2n 的长方形，沿图中虚线用剪刀将其均分成四个完全相同的小长方形，然后按图 2 的形状拼图．
(1)图 2 中的图形阴影部分的边长为 ；(用含 m、n 的代数式表示)
(2)请你用两种不同的方法分别求图 2 中阴影部分的面积； 方法一： ；方法二： ．
(3)观察图 2，请写出代数式(m+n)2、(m﹣n)2、4mn 之间的关系式： ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了鼓励市民节约用水，某市水费实行阶梯式计量水价.每户每月用水量不超过25吨，收
费标准为每吨a元；若每户每月用水量超过25吨时，其中前25吨还是每吨a元，超出的部
分收费标准为每吨b元．下表是小明家一至四月份用水量和缴纳水费情况.根据表格提供的数
据，回答：
月份
一
二
三
四
用水量（吨）
16
18
30
35
水费（元）
32
36
65
80
（1）a=________；b=________；
（2）若小明家五月份用水32吨，则应缴水费 元；
（3）若小明家六月份应缴水费102.5元，则六月份他们家的用水量是多少吨？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某政府大力扶持大学生创业．李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯．物价部门规定，这种护眼台灯的销售单价不得高于32元．销售过程中发现，月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：y=﹣10x+n．
（1）当销售单价x定为25元时，李明每月获得利润为w为1250元，则n=；
（2）如果李明想要每月获得2000元的利润，那么销售单价应定为多少元？
（3）当销售单价定为多少元时，每月可获得最大利润？并求最大利润为多少元． -
科目： 来源： 题型：
查看答案和解析>>【题目】先阅读下面的例题，再解答后面的题目．
例：已知x2+y2﹣2x+4y+5＝0，求x+y的值．
解：由已知得（x2﹣2x+1）+（y2+4y+4）＝0，
即（x﹣1）2+（y+2）2＝0．
因为（x﹣1）2≥0，（y+2）2≥0，它们的和为0，
所以必有（x﹣1）2＝0，（y+2）2＝0，
所以x＝1，y＝﹣2．
所以x+y＝﹣1．
题目：已知x2+4y2﹣6x+4y+10＝0，求xy的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】 如图，正方形网格中的每个小正方形的边长都是1，每个小正方形的顶点叫作格点．△ABC的三个顶点A，B，C都在格点上，将△ABC绕点A按顺时针方向旋转90°得到△AB′C′．
（1）在正方形网格中，画出△AB'C′；
（2）画出△AB′C′向左平移4格后的△A′B″C″；
（3）计算线段AB在变换到AB′的过程中扫过区域的面积．
相关试题
