搜索
【题目】已知：如图，AB是⊙O的直径，弦 
，∠B=60°，OD⊥AC，垂足为D．
（1）求OD的长；
（2）求劣弧AC的长．
参考答案：
【答案】
（1）解：∵AB是⊙O的直径，
∴∠C=90°，
又∵OD⊥AC，
∴AD=CD= 
，∠ADO=90°，
∵∠B=60°
∴∠A=30°，
在Rt△AOD中，OA=2，OD=1
（2）解：连接OC，
则∠AOC=120°，
∴ 
的长l= 
= 
= 
．
【解析】（1）根据圆周角定理证得△ABC是直角三角形，再根据垂径定理求出AD的长及∠A的度数，然后在Rt△AOD中，利用解直角三角形就可求出OD的长；或根据三角形的中位线定理也可求出结果。
（2）要求劣弧AC的长，只需求出圆心角∠AOC的度数，再利用弧长公式计算即可。
【考点精析】认真审题，首先需要了解垂径定理(垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧)，还要掌握圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半)的相关知识才是答题的关键．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）填空：31﹣30＝3（ ）×2，32﹣31＝3（ ）×2，33﹣32＝3 （ ）×2，…
（2）探索（1）中式子的规律，试写出第n个等式，并说明第n个等式成立；
（3）计算：3+32+33+…+32018．
-
科目： 来源： 题型：
查看答案和解析>>【题目】A城气象台测得台风中心在A城正西方向320km的B处，以每小时40km的速度向北偏东60°的BF方向移动，距离台风中心200km的范围内是受台风影响的区域．
（1）自己画出图形并解答：A城是否受到这次台风的影响？为什么？
（2）若A城受到这次台风影响，那么A城遭受这次台风影响有多长时间？
-
科目： 来源： 题型：
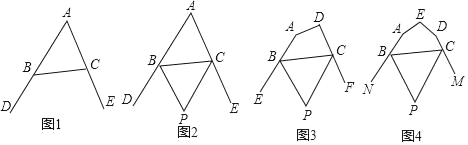
查看答案和解析>>【题目】（1）如图1，在△ABC中，∠DBC与∠ECB分别为△ABC的两个外角，若∠A＝60°，∠DBC+∠ECB多少度；
（2）如图2，在△ABC中，BP、CP分别平分外角∠DBC、∠ECB，∠P与∠A有怎样的数量关系？为什么？
（3）如图3，在四边形ABCD中，BP、CP分别平分外角∠EBC、∠FCB，∠P与∠A+∠D有怎样的数量关系？为什么？
（4）如图4，在五边形ABCDE中，BP、CP分别平分外角∠NBC、∠MCB，∠P与∠A+∠D+∠E有怎样的数量关系？(直接写出答案)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】麒麟区第七中学现有一块空地ABCD如图所示，现计划在空地上种草皮，经测量，∠B=90°，AB=3m，BC=4m，CD=13m，AD=12m．
（1）求出空地ABCD的面积？
（2）若每种植1平方米草皮需要300元，问总共需投入多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知在平面直角坐标系xOy中，O是坐标原点，点A（2，5）在反比例函数y=
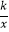的图象上，过点A的直线y=x+b交x轴于点B．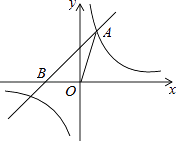
（1）求k和b的值；
（2）求△OAB的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】△ABC中，∠A，∠B，∠C的对边分别为a、b、c，下列说法中错误的是（ ）
A．如果∠C－∠B＝∠A，则△ABC是直角三角形，且∠C＝90；
B．如果
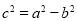，则△ABC是直角三角形，且∠C＝90；C．如果（c＋a）（ c－a）＝
，则△ABC是直角三角形，且∠C＝90；D．如果∠A：∠B：∠C＝3：2：5，则△ABC是直角三角形，且∠C＝90．
相关试题
