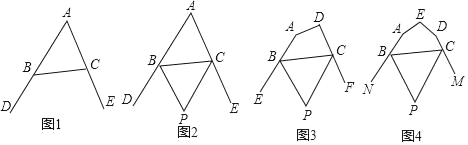
【题目】(1)如图1,在△ABC中,∠DBC与∠ECB分别为△ABC的两个外角,若∠A=60°,∠DBC+∠ECB多少度;
(2)如图2,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有怎样的数量关系?为什么?
(3)如图3,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,∠P与∠A+∠D有怎样的数量关系?为什么?
(4)如图4,在五边形ABCDE中,BP、CP分别平分外角∠NBC、∠MCB,∠P与∠A+∠D+∠E有怎样的数量关系?(直接写出答案).
参考答案:
【答案】(1)∠DBC+∠ECB=240°;(2)∠P=90°﹣![]() ∠A;(3)∠P=180°﹣
∠A;(3)∠P=180°﹣![]() (∠A+∠D)(4)∠P=270°﹣
(∠A+∠D)(4)∠P=270°﹣![]() (∠A+∠E+∠D).
(∠A+∠E+∠D).
【解析】
(1)根据三角形内角和定理求出∠ABC+∠ACB,根据外角的性质计算;(2)根据角平分线的定义得到∠PBC=![]() ∠DBC,∠PCB=
∠DBC,∠PCB=![]() ∠ECB,根据三角形内角和定理计算;
∠ECB,根据三角形内角和定理计算;
(3)根据四边形内角和等于360°计算;(4)根据五边形的内角和等于540°、三角形的外角的性质、角平分线的定义计算.
(1)∵∠A=60°,
∴∠ABC+∠ACB=180°﹣60°=120°,
∴∠DBC+∠ECB=360°﹣120°=240°;
(2)∵BP、CP分别平分外角∠DBC、∠ECB,
∴∠PBC=![]() ∠DBC,∠PCB=
∠DBC,∠PCB=![]() ∠ECB,
∠ECB,
∴∠ABC+∠ACB=180°﹣∠A,
∴∠DBC+∠ECB=360°﹣(180°﹣∠A)=180°+∠A,
∴∠PBC+∠PCB=90°+![]() ∠A,
∠A,
∴∠P=180°﹣(∠PBC+∠PCB)=90°﹣![]() ∠A;
∠A;
(3)∴∠ABC+∠ACB=360°﹣∠A﹣∠D,
∴∠DBC+∠ECB=360°﹣(360°﹣∠A﹣∠D)=∠A+∠D,
∴∠PBC+∠PCB=![]() (∠A+∠D),
(∠A+∠D),
∴∠P=180°﹣![]() (∠A+∠D);
(∠A+∠D);
(4)五边形的内角和=(5﹣2)×180°=540°,
∴∠ABC+∠ACB=540°﹣∠A﹣∠E﹣∠D,
∴∠DBC+∠ECB=360°﹣(540°﹣∠A﹣∠E﹣∠D)=∠A+∠E+∠D﹣180°,
∴∠PBC+∠PCB=![]() (∠A+∠E+∠D﹣180°),
(∠A+∠E+∠D﹣180°),
∠P=180°﹣![]() (∠A+∠E+∠D﹣180°)=270°﹣
(∠A+∠E+∠D﹣180°)=270°﹣![]() (∠A+∠E+∠D).
(∠A+∠E+∠D).
-
科目: 来源: 题型:
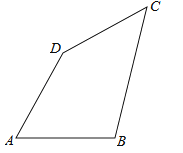
查看答案和解析>>【题目】在四边形ABCD中,AB=AD=8,∠A=60°,∠D=150°,四边形周长为32,求BC和CD的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)填空:31﹣30=3( )×2,32﹣31=3( )×2,33﹣32=3 ( )×2,…
(2)探索(1)中式子的规律,试写出第n个等式,并说明第n个等式成立;
(3)计算:3+32+33+…+32018.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A城气象台测得台风中心在A城正西方向320km的B处,以每小时40km的速度向北偏东60°的BF方向移动,距离台风中心200km的范围内是受台风影响的区域.
(1)自己画出图形并解答:A城是否受到这次台风的影响?为什么?
(2)若A城受到这次台风影响,那么A城遭受这次台风影响有多长时间?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB是⊙O的直径,弦
 ,∠B=60°,OD⊥AC,垂足为D.
,∠B=60°,OD⊥AC,垂足为D.
(1)求OD的长;
(2)求劣弧AC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】麒麟区第七中学现有一块空地ABCD如图所示,现计划在空地上种草皮,经测量,∠B=90°,AB=3m,BC=4m,CD=13m,AD=12m.

(1)求出空地ABCD的面积?
(2)若每种植1平方米草皮需要300元,问总共需投入多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=
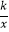 的图象上,过点A的直线y=x+b交x轴于点B.
的图象上,过点A的直线y=x+b交x轴于点B.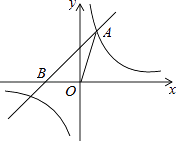
(1)求k和b的值;
(2)求△OAB的面积.
相关试题

