【题目】如图,已知在△ABC中,∠C=90°,AB的垂直平分线MN交BC于点D.
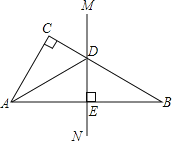
(1)如果∠CAD=20°,求∠B的度数;
(2)如果∠CAB=50°,求∠CAD的度数;
(3)如果∠CAD:∠DAB=1:2,求∠CAB的度数.
参考答案:
【答案】(1)∠B=35°;(2)∠CAD=10°;(3)∠CAB=54°.
【解析】试题分析:(1)根据直角三角形的性质求出∠ADC=70°,根据线段的垂直平分线的性质得到DA=DB,计算即可;
(2)根据直角三角形的性质求出∠B的度数,根据线段的垂直平分线的性质得到DA=DB,计算即可;
(3)设∠CAD=x,根据题意列出方程,解方程即可.
试题解析:(1)∵∠C=90°,∠CAD=20°,
∴∠ADC=70°,
∵DE是AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠B=35°,
答:∠B的度数是35°;
(2)∵∠C=90°,∠CAB=50°,
∴∠B=40°,
∵DE是AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠B=40°,
∴∠CAD=10°;
(3)设∠CAD=x,则∠DAB=∠B=2x,
则x+2x+2x=90°,
解得x=18,
则∠CAB=54°.
-
科目: 来源: 题型:
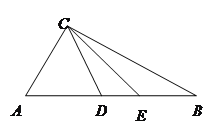
查看答案和解析>>【题目】如图,△ABC中,D、E在AB上,且D、E分别是AC、BC的垂直平分线上一点;若△CDE的周长为4,则AB的长为___________;若∠ACB=100°,则∠DCE=_________度;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△BOD都是等腰直角三角形,∠ACB=∠BDO=90°,且点A在反比例函数
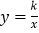 (k>0)的图像上,若OB2-AB2=10,则k的值为 ( )
(k>0)的图像上,若OB2-AB2=10,则k的值为 ( )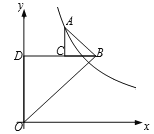
A. 10 B. 5 C. 20 D. 2.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,BC=12,∠B=30°,AB的垂直平分线DE交BC边于点E,AC的垂直平分线MN交BC于点N.
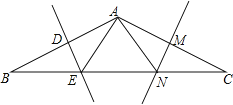
(1)求△AEN的周长;
(2)求证:BE=EN=NC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣(x+1)(x﹣m)交x轴于A,B两点(A在B的左侧,m>0),交y轴正半轴于点C,过点C作x轴的平行线交抛物线于另一点E,抛物线的对称轴交CE于点F,以C为圆心画圆,使⊙C经过点(0,2).
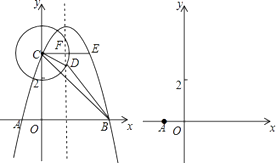
(1)直接写出OB,OC的长.(均用含m的代数式表示)
(2)当m>2时,判断点E与⊙C的位置关系,并说明理由.
(3)当抛物线的对称轴与⊙C相交时,其中下方的交点为D.连结CD,BD,BC.
①当m>3,且C,D,B三点在同一直线上时,求m的值.
②当△BCD是以CD为腰的等腰三角形时,求m的值.(直接写出答案即可) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图,其中每个小正方形的边长为1个单位长度.
(1)按要求作图:
①画出△ABC关于原点O的中心对称图形△A1B1C1;
②画出将△ABC绕点C顺时针旋转90°得到△A2B2C2.
(2)回答下列问题:
①△A1B1C1中顶点A1坐标为 ;
②若P(a,b)为△ABC边上一点,则按照(1)中①作图,点P对应的点P1的坐标为 .

相关试题

