【题目】已知函数图象如图所示,根据图象可得: 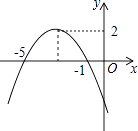
(1)抛物线顶点坐标;
(2)对称轴为
(3)当x=时,y有最大值是;
(4)当时,y随着x得增大而增大.
(5)当时,y>0.
参考答案:
【答案】
(1)(﹣3,2)
(2)x=﹣3
(3)-3;2
(4)x<﹣3
(5)﹣5<x<﹣1
【解析】解:(1)∵抛物线与x轴交于点(﹣5,0),(﹣1,0),
∴顶点横坐标为 ![]() =﹣3,
=﹣3,
由图可知顶点纵坐标为2,
∴顶点坐标为(﹣3,2);(2)对称轴为x=﹣3;(3)当x=﹣3时,y有最大值是2;(4)当x<﹣3时,y随着x得增大而增大;(5)当﹣5<x<﹣1时,y>0.
所以答案是(1)(﹣3,2);(2)x=﹣3;(3)﹣3,2;(4)x<﹣3;(5)﹣5<x<﹣1.
【考点精析】根据题目的已知条件,利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下面给出的数轴中,点 A 表示 1,点 B 表示-2,回答下面的问题:
(1)A、B 之间的距离是 ;
(2)观察数轴,与点 A 的距离为 5 的点表示的数是: ;
(3)若将数轴折叠,使点 A 与-3 表示的点重合,则点 B 与数 表示的点重合;
(4)若数轴上 M、N 两点之间的距离为 2018(M 在 N 的左侧),且 M、N 两点经过(3)中折 叠 后 互 相 重 合 , 则 M 、 N 两 点 表 示 的 数 分 别 是 : M : ;N: .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过反比例函数y=
 (x>0)的图象上一点A作x轴的平行线,交双曲线y=-
(x>0)的图象上一点A作x轴的平行线,交双曲线y=- (x<0)于点B,过B作BC∥OA交双曲线y=-
(x<0)于点B,过B作BC∥OA交双曲线y=- (x<0)于点D,交x轴于点C,连接AD交y轴于点E,若OC=3,求OE的长.
(x<0)于点D,交x轴于点C,连接AD交y轴于点E,若OC=3,求OE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=3a2b﹣2ab2+abc,小明同学错将“2A﹣B“看成”2A+B“,算得结果为4a2b﹣3ab2+4abc.
(1)计算B的表达式;
(2)求出2A﹣B的结果;
(3)小强同学说(2)中的结果的大小与c的取值无关,对吗?若a=
 ,b=
,b= ,
,求(2)中式子的值.
-
科目: 来源: 题型:
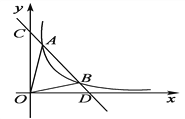
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
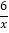 (x>0)的图象交于A(m,6),B(3,n)两点.
(x>0)的图象交于A(m,6),B(3,n)两点.(1)求一次函数的解析式;
(2)根据图象直接写出kx+b-
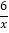 <0时x的取值范围;
<0时x的取值范围;(3)求△AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=mx+5的图象与反比例函数y=
 (k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M.
(k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M.(1)求一次函数和反比例函数的解析式;
(2)求△OAM的面积S;
(3)在y轴上求一点P,使PA+PB最小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.

(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)若抛物线上有一动点P,使三角形ABP的面积为6,求P点坐标.
相关试题

