【题目】已知:如图,抛物线y=ax2+bx﹣3与x轴交于A、B两点,与y轴交于点C,O是坐标原点,已知点B的坐标是(3,0),tan∠OAC=3;
(1)求该抛物线的函数表达式;
(2)点P在x轴上方的抛物线上,且∠PAB=∠CAB,求点P的坐标;
(3)若平行于x轴的直线与抛物线交于点M、N(M点在N点左侧),
①若以MN为直径的圆与x轴相切,求该圆的半径;
②若Q(m,4)是直线MN上一动点,当以点C、B、Q为顶点的三角形的面积等于6时,请直接写出符合条件的m值,为 .
参考答案:
【答案】
(1)
解:∵抛物线y=ax2+bx﹣3与y轴交于点C,
∴点C的坐标为(0,﹣3),
∴OC=3,
∵tan∠OAC=3,
∴OA=1,即点A的坐标为(﹣1,0),
将点A和点B的坐标代入得: ![]() ,解得
,解得 ![]() ,
,
∴抛物线的函数表达式是y=x2﹣2x﹣3
(2)
解:∵∠PAB=∠CAB,
∴tan∠PAB=tan∠CAB=3,
∵点P在x轴上方,设点P的横坐标为x,则点P的纵坐标为3(x+1),
∴3(x+1)=x2﹣2x﹣3,得x=﹣1(舍去)或x=6,当x=6时,y=21,
∴点P的坐标为(6,21)
(3)3或11
【解析】解:(3)∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线的对称轴为直线x=1.
①当直线MN在x轴上方时,设圆的半径为R(R>0),则N(R+1,R),
∴R=( R+1﹣1)2﹣4,解得:R= ![]() (负值舍去),
(负值舍去),
∴R= ![]() .
.
当直线MN在x轴下方时,设圆的半径为r(r>0),
∴N(r+1,﹣r),
∴﹣r=(r+1﹣1)2﹣4,解得:r= ![]() (负值舍去),
(负值舍去),
∴r= ![]() ,
,
∴圆的半径为: ![]() 或
或 ![]() .
.
②设直线BC的解析式为y=kx+b,将点C和点B的坐标代入得: ![]() ,
,
解得k=1,b=﹣3,
∴直线BC的解析式为y=x﹣3.
勾股定理可知:BC= ![]() =3
=3 ![]() .
.
∵△QCB的面积为6,
∴BC边上的高线的长度= ![]() =2
=2 ![]() .
.
如图1所示:即直线BC与y=4的交点为D,当点Q在点D的左侧时,过点Q作QE⊥BC,则EQ=2 ![]()

将y=0代入得直线BC的解析式得:x﹣3=4,解得x=7,
∴点D的坐标为(7,4).
∵QD∥x轴,
∴∠QDC=∠OBC=45°.
∴QD= ![]() QE=
QE= ![]() ×2
×2 ![]() =4.
=4.
∴Q(3,4).
∴m=3.
如图1所示,当Q位于点D的右侧时(Q′处),过点Q′作Q′F⊥BC,垂足为F.则FQ=2 ![]() ,
,
同理可知:DQ′=4.
∴点Q′的坐标为(11,4).
∴m=11.
综上所述,m的值为3或11.
所以答案是:3或11.
【考点精析】认真审题,首先需要了解二次函数的概念(一般地,自变量x和因变量y之间存在如下关系:一般式:y=ax2+bx+c(a≠0,a、b、c为常数),则称y为x的二次函数).
-
科目: 来源: 题型:
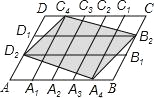
查看答案和解析>>【题目】在平行四边形ABCD中,点A1,A2,A3,A4和C1,C2,C3,C4分别AB和CD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为1,则平行四边形ABCD面积为( )
A. 2 B.
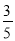 C.
C.  D. 15
D. 15 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),已知小正方形 ABCD 的面积为1,把它的各边延长一倍得到新正方形 A 1 B 1 C 1 D 1 ;把正方形 A 1 B 1 C 1 D 1 边长按原法延长一倍得到正方形 A 2 B 2 C 2 D 2 (如图(2));以此下去,则正方形 A n B n C n D n 的面积为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下面图形都是由同样大小的平行四边形按一定的规律组成,其中,第①个图形一共有1个平行四边形,第②个图形一共有5个平形四边形,第③个图形一共有11个平行四边形,……,则第⑥个图形中平行四边形的个数为__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果100个乒乓球中有20个红色的,那么在随机抽出的20个乒乓球中( )
A.刚好有4个红球
B.红球的数目多于4个
C.红球的数目少于4个
D.以上都有可能 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,BC=5,AB=3,分别经过点B和点D的两个动圆均与AC相切,且与AB、BC、AD、DC分别交于点G、H、E、F,则EF+GH的最小值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列网格中建立平面直角坐标系如图,每个小正方形的边长均为1个单位长度.已知A(1,1)、B(3,4)和C(4,2).
(1)在图中标出点A、B、C.
(2)将点C向下平移3个单位到D点,将点A先向左平移3个单位,再向下平移1个单位到E点,在图中标出D点和E点.
(3)求△EBD的面积S△EBD.

相关试题

