【题目】如图,在△ABC 中,AB=AC,AE 是∠BAC 的平分线,∠ABC 的平分线 BM 交 AE 于点 M,点 O在 AB 上,以点O 为圆心,OB 的长为半径的圆经过点 M,交 BC 于点G,交 AB 于点 F.
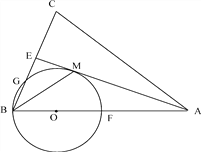
(1)求证:AE 为⊙O 的切线.
(2)当 BC=8,AC=12 时,求⊙O 的半径.
(3)在(2)的条件下,求线段 BG 的长.
参考答案:
【答案】(1)证明见解析(2)3(3)2
【解析】分析:(1)连接OM.利用角平分线的性质和平行线的性质得到AE⊥OM,后即可证得AE是![]() 的切线;
的切线;
(2)设![]() 的半径为r,根据OM∥BE,得到△OMA∽△BEA,利用平行线的性质得到
的半径为r,根据OM∥BE,得到△OMA∽△BEA,利用平行线的性质得到
![]() ,即可解得
,即可解得![]() ,
,![]() 的半径为3;
的半径为3;
(3)过点O作OH⊥BG于点H,则BG=2BH,根据![]() 得到四边形OMEH是矩形,从而得到HE=OM=3和BH=1,证得结论BG=2BH=2.
得到四边形OMEH是矩形,从而得到HE=OM=3和BH=1,证得结论BG=2BH=2.
详解:(1)证明:连接OM.

∵AC=AB,AE平分∠BAC,
∴AE⊥BC,![]()
∵OB=OM,
∴∠OBM=∠OMB,
∵BM平分∠ABC,
∴∠OBM=∠CBM,
∴∠OMB=∠CBM,
∴OM∥BC
又∵AE⊥BC,
∴AE⊥OM,
∴AE是![]() 的切线;
的切线;
(2)设![]() 的半径为r,
的半径为r,
∵OM∥BE,
∴△OMA∽△BEA,
∴![]() 即
即![]() ,
,
解得![]()
∴![]() 的半径为3;
的半径为3;
(3)过点O作OH⊥BG于点H,则BG=2BH,
∵![]()
∴四边形OMEH是矩形,
∴HE=OM=3,
∴BH=1,
∴BG=2BH=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】华生电器商场在“双11购物节”期间进行“现金返还”活动,凡购买指定家用电器的购买者均可得到该商品售价18%的返还现金.小芳家购买了一台
 型洗衣机,小明家购买了一台
型洗衣机,小明家购买了一台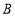 型洗衣机,两家一共得到返还现金1170元,又知
型洗衣机,两家一共得到返还现金1170元,又知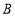 型洗衣机比
型洗衣机比 型洗衣机售价高500元.
型洗衣机售价高500元.(1)
 型洗衣机和
型洗衣机和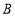 型洗衣机的售价各是多少元?
型洗衣机的售价各是多少元?(2)小芳家和小明家购买洗衣机时除返还现金外实际各付款多少元?
-
科目: 来源: 题型:
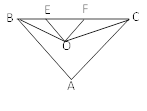
查看答案和解析>>【题目】如图,已知BO、CO分别是∠ABC和∠ACB的平分线,OE∥AB,OF∥AC,如果已知BC的长为a,你能知道△OEF的周长吗?算算看.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:如果矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形.例如,下图中的矩形A1B1C1D1,A2B2C2D2,AB3C3D3都是点A,B,C的覆盖矩形,其中矩形AB3C3D3是点A,B,C的最优覆盖矩形.

(1)已知A(
 2,3),B(5,0),C(
2,3),B(5,0),C( ,
,  2).
2).①当
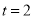 时,点A,B,C的最优覆盖矩形的面积为 ;
时,点A,B,C的最优覆盖矩形的面积为 ;②若点A,B,C的最优覆盖矩形的面积为40,则t的值为 ;
(2)已知点D(1,1),点E(
 ,
,  ),其中点E是函数
),其中点E是函数 的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线ykx3经过点B(-
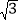 ,2),且与 x 轴交于点A.将抛物线
,2),且与 x 轴交于点A.将抛物线 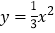 沿 x 轴作左右平移,记平移后的抛物线为C,其顶点为P.
沿 x 轴作左右平移,记平移后的抛物线为C,其顶点为P.(1)求∠OAB 的度数;
(2)抛物线
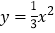 与直线 ykx3相交于 M,N两点,求△MON的面积.
与直线 ykx3相交于 M,N两点,求△MON的面积.(3)在抛物线
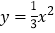 平移过程中,将△PAB 沿直线 AB 翻折得到△DAB,点D 能否落在抛物线C 上?如能,求出此时抛物线C 顶点P 的坐标;如不能,说明理由.
平移过程中,将△PAB 沿直线 AB 翻折得到△DAB,点D 能否落在抛物线C 上?如能,求出此时抛物线C 顶点P 的坐标;如不能,说明理由.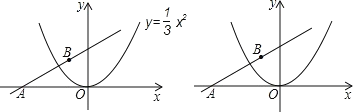
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两辆汽车同时从相距330千米的甲、乙两地相向而行,s(千米)表示汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,L1,L2分别表示两辆汽车的s与t的关系.
(1)L1表示哪辆汽车到甲地的距离与行驶时间的关系?
(2)汽车B的速度是多少?
(3)求L1,L2分别表示的两辆汽车的s与t的关系式.
(4)2小时后,两车相距多少千米?
(5)行驶多长时间后,A、B两车相遇?

-
科目: 来源: 题型:
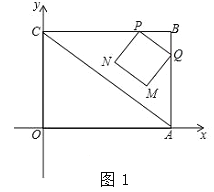
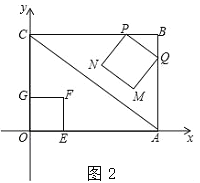
查看答案和解析>>【题目】已知矩形OABC在如图所示平面直角坐标系中,点B的坐标为(4,3),连接AC.动点P从点B出发,以2cm/s的速度,沿直线BC方向运动,运动到C为止(不包括端点B、C),过点P作PQ∥AC交线段BA于点Q,以PQ为边向下作正方形PQMN,设正方形PQMN与△ABC重叠部分图形面积为S(cm2),设点P的运动时间为t(s).
(1)请用含t的代数式表示BQ长和N点的坐标;
(2)求S与t之间的函数关系式,并指出t的取值范围;
(3)如图2,点G在边OC上,且OG=1cm,在点P从点B出发的同时,另有一动点E从点O出发,以2cm/s的速度,沿x轴正方向运动,以OG、OE为一组邻边作矩形OEFG.试求当点F落在正方形PQMN的内部(不含边界)时t的取值范围.
相关试题

