【题目】如图,直线ykx3经过点B(-![]() ,2),且与 x 轴交于点A.将抛物线
,2),且与 x 轴交于点A.将抛物线 ![]() 沿 x 轴作左右平移,记平移后的抛物线为C,其顶点为P.
沿 x 轴作左右平移,记平移后的抛物线为C,其顶点为P.
(1)求∠OAB 的度数;
(2)抛物线![]() 与直线 ykx3相交于 M,N两点,求△MON的面积.
与直线 ykx3相交于 M,N两点,求△MON的面积.
(3)在抛物线![]() 平移过程中,将△PAB 沿直线 AB 翻折得到△DAB,点D 能否落在抛物线C 上?如能,求出此时抛物线C 顶点P 的坐标;如不能,说明理由.
平移过程中,将△PAB 沿直线 AB 翻折得到△DAB,点D 能否落在抛物线C 上?如能,求出此时抛物线C 顶点P 的坐标;如不能,说明理由.
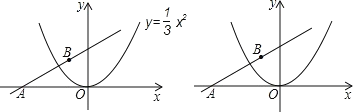
参考答案:
【答案】(1)30°(2)![]() (3)(3
(3)(3![]() ,0)
,0)
【解析】分析:(1)点B在直线AB上,所以把B点坐标代入解析式即可求出未知数的值,进而求出其解析式.根据直线解析式可求出A点的坐标及直线与y轴交点的坐标,根据锐角三角函数的定义即可求出∠BAO的度数.
(2)设![]() 联立
联立 消去y,得到
消去y,得到![]() ,则
,则![]() ,
,![]() ,
,![]() ,即可求得
,即可求得![]() .
.
(3)根据特殊角求出D点的坐标表达式,将表达式代入解析式,看能否计算出P点坐标,若能,则D点在抛物线C上.反之,不在抛物线上.
详解:(1)∵点B在直线AB上,求得b=3,
∴直线AB:![]() ,
,
∴A(![]() ,0),即OA=
,0),即OA=![]() .
.
当![]() 时,直线AB:
时,直线AB:![]() 与
与![]() 轴交于点
轴交于点![]()
∴![]() .
.
(2) 设![]()
联立 消去y,得到
消去y,得到![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 于y轴相交于(0,3)
于y轴相交于(0,3)
∴![]()
(3)假设点D落在抛物线C上,
不妨设此时抛物线顶点P(t,0),则抛物线C:![]() ,AP=
,AP=![]() + t,
+ t,
连接DP,作DM⊥x轴,垂足为M.由已知,得△PAB≌△DAB,
又∠BAO=30°,∴△PAD为等边三角形.PM=AM=![]() ,
,
∴![]()
![]() ,
,
![]() .
.
∵点D落在抛物线C上,
∴![]()
当![]() 时,此时点P
时,此时点P![]() ,点P与点A重合,不能构成三角形,不符合题意,舍去.所以点P为(
,点P与点A重合,不能构成三角形,不符合题意,舍去.所以点P为(![]() ,0)
,0)
∴当点D落在抛物线C上顶点P为(![]() ,0).
,0).
-
科目: 来源: 题型:
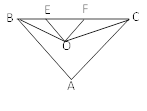
查看答案和解析>>【题目】如图,已知BO、CO分别是∠ABC和∠ACB的平分线,OE∥AB,OF∥AC,如果已知BC的长为a,你能知道△OEF的周长吗?算算看.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:如果矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形.例如,下图中的矩形A1B1C1D1,A2B2C2D2,AB3C3D3都是点A,B,C的覆盖矩形,其中矩形AB3C3D3是点A,B,C的最优覆盖矩形.

(1)已知A(
 2,3),B(5,0),C(
2,3),B(5,0),C( ,
,  2).
2).①当
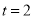 时,点A,B,C的最优覆盖矩形的面积为 ;
时,点A,B,C的最优覆盖矩形的面积为 ;②若点A,B,C的最优覆盖矩形的面积为40,则t的值为 ;
(2)已知点D(1,1),点E(
 ,
,  ),其中点E是函数
),其中点E是函数 的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,AB=AC,AE 是∠BAC 的平分线,∠ABC 的平分线 BM 交 AE 于点 M,点 O在 AB 上,以点O 为圆心,OB 的长为半径的圆经过点 M,交 BC 于点G,交 AB 于点 F.
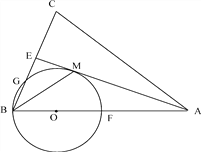
(1)求证:AE 为⊙O 的切线.
(2)当 BC=8,AC=12 时,求⊙O 的半径.
(3)在(2)的条件下,求线段 BG 的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两辆汽车同时从相距330千米的甲、乙两地相向而行,s(千米)表示汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,L1,L2分别表示两辆汽车的s与t的关系.
(1)L1表示哪辆汽车到甲地的距离与行驶时间的关系?
(2)汽车B的速度是多少?
(3)求L1,L2分别表示的两辆汽车的s与t的关系式.
(4)2小时后,两车相距多少千米?
(5)行驶多长时间后,A、B两车相遇?

-
科目: 来源: 题型:
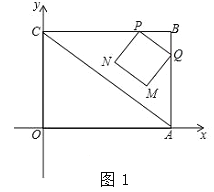
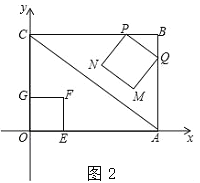
查看答案和解析>>【题目】已知矩形OABC在如图所示平面直角坐标系中,点B的坐标为(4,3),连接AC.动点P从点B出发,以2cm/s的速度,沿直线BC方向运动,运动到C为止(不包括端点B、C),过点P作PQ∥AC交线段BA于点Q,以PQ为边向下作正方形PQMN,设正方形PQMN与△ABC重叠部分图形面积为S(cm2),设点P的运动时间为t(s).
(1)请用含t的代数式表示BQ长和N点的坐标;
(2)求S与t之间的函数关系式,并指出t的取值范围;
(3)如图2,点G在边OC上,且OG=1cm,在点P从点B出发的同时,另有一动点E从点O出发,以2cm/s的速度,沿x轴正方向运动,以OG、OE为一组邻边作矩形OEFG.试求当点F落在正方形PQMN的内部(不含边界)时t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线 y=kx+b(k≠0)过点 F(0,1),与抛物线
 相交于B、C 两点
相交于B、C 两点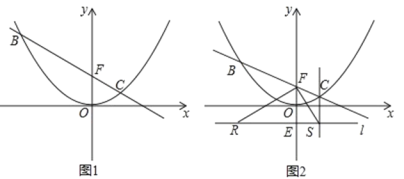
(1)如图 1,当点 C 的横坐标为 1 时,求直线 BC 的解析式;
(2)在(1)的条件下,点 M 是直线 BC 上一动点,过点 M 作 y 轴的平行线,与抛物线交于点 D, 是否存在这样的点 M,使得以 M、D、O、F 为顶点的四边形为平行四边形?若存在,求出点 M 的坐标;若不存在,请说明理由;
(3)如图 2,设 B(m,n)(m<0),过点 E(0,-1)的直线 l∥x 轴,BR⊥l 于 R,CS⊥l 于 S,连接 FR、FS.试判断△ RFS 的形状,并说明理由.
相关试题

