【题目】探究题
已知:如图1,![]() ,
,![]() .求证:
.求证:![]() .
.

老师要求学生在完成这道教材上的题目证明后,尝试对图形进行变式,继续做拓展探究,看看有什么新发现?
(1)小颖首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小颖用到的平行线性质可能是 .
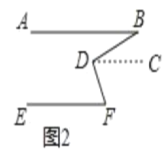
(2)接下来,小颖用《几何画板》对图形进行了变式,她先画了两条平行线![]() ,然后在平行线间画了一点
,然后在平行线间画了一点![]() ,连接
,连接![]() 后,用鼠标拖动点
后,用鼠标拖动点![]() ,分别得到了图2,3,4,小颖发现图3正是上面题目的原型,于是她由上题的结论猜想到图2和4中的
,分别得到了图2,3,4,小颖发现图3正是上面题目的原型,于是她由上题的结论猜想到图2和4中的![]() 、
、![]() 与
与![]() 之间也可能存在着某种数量关系.于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
之间也可能存在着某种数量关系.于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
请你在小颖操作探究的基础上,继续完成下面的问题:
①猜想图2中![]() 、
、![]() 与
与![]() 之间的数量关系并加以证明;
之间的数量关系并加以证明;
②补全图4,直接写出![]() 、
、![]() 与
与![]() 之间的数量关系.
之间的数量关系.
参考答案:
【答案】(1)两直线平行同旁内角互补;(2)①∠BDF=∠B+F;②∠F=∠B+∠BDF
【解析】
(1)根据两直线平行同旁内角互补即可解决问题;
(2)①猜想∠BDF=∠B+∠F.过点D作CD//AB.利用平行线的性质即可解决问题;
②∠BDF与∠F之间的数量关系是∠F=∠B+∠BDF.利用平行线的性质已经三角形的外角的性质即可解决问题;
.
:(1)两直线平行同旁内角互补.
故答案为两直线平行同旁内角互补.
(2)①猜想∠BDF=∠B+∠F.
证明:过点D作CD//AB.
∴∠B=∠BDC.
∵AB//EF,∴CD//EF.
∴∠CDF=∠F.
∵∠BDF=∠BDC+∠CDF,
∴∠BDF=∠B+F.
②补全图形如图所示:∠B、∠BDF与∠F之间的数量关系是∠F=∠B+∠BDF.
理由:∵AB//EF,
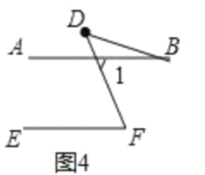
∴∠1=∠F,
∵∠1=∠B+∠D,
∴∠F=∠B+∠BDF.
故答案为∠F=∠B+∠BDF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】统计七年级部分同学的跳高测试成绩,得到如下频率直方图(每组含前一个边界值,不含后一个边界值).

(1)参加测试的总人数是多少人?
(2)组距为多少?
(3)跳高成绩在
 (含
(含 )以上的有多少人?占总人数的百分之几?
)以上的有多少人?占总人数的百分之几? -
科目: 来源: 题型:
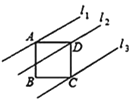
查看答案和解析>>【题目】如图,直线l1,l2,l3分别过正方形ABCD的三个顶点A,D,C,且相互平行,若l1,l2的距离为2,l2,l3的距离为4,则正方形的对角线长为_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若抛物线L:y=ax2+bx+c(a,b,c是常数,abc≠0)与直线l都经过y轴上的一点P,且抛物线L的顶点Q在直线l上,则称此直线l与该抛物线L具有“一带一路”关系.此时,直线l叫做抛物线L的“带线”,抛物线L叫做直线l的“路线”.
(1)若直线y=mx+1与抛物线y=x2﹣2x+n具有“一带一路”关系,求m,n的值;
(2)若某“路线”L的顶点在反比例函数y=
 的图象上,它的“带线”l的解析式为y=2x﹣4,求此“路线”L的解析式;
的图象上,它的“带线”l的解析式为y=2x﹣4,求此“路线”L的解析式;(3)当常数k满足
 ≤k≤2时,求抛物线L:y=ax2+(3k2﹣2k+1)x+k的“带线”l与x轴,y轴所围成的三角形面积的取值范围.
≤k≤2时,求抛物线L:y=ax2+(3k2﹣2k+1)x+k的“带线”l与x轴,y轴所围成的三角形面积的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级举行“数学计算能力”比赛,比赛结束后,随机抽查部分学生的成绩,根据抽查结果绘制成如下的统计图表
组别
分数x
频数
A
40≤x<50
20
B
50≤x<60
30
C
60≤x<70
50
D
70≤x<80
m
E
80≤x<90
40
根据以上信息解答下列问题:
(1)共抽查了 名学生,统计图表中,m= ,请补全直方图;
(2)求扇形统计图中“B组”所对应的圆心角的度数;
(3)若七年级共有800名学生,分数不低于60分为合格,请你估算本次比赛全年级合
格学生的人数

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 ABCD中,O是对角线AC的中点,过点O作AC的垂线与边AD、BC分别交于E、F.四边形AFCE是菱形吗?请说明理由.
ABCD中,O是对角线AC的中点,过点O作AC的垂线与边AD、BC分别交于E、F.四边形AFCE是菱形吗?请说明理由.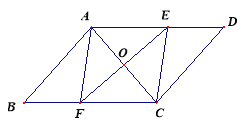
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(0,4),B(3,0),线段AB平移后对应的线段为CD,点C在x轴的负半轴上,B、C两点之间的距离为8.
(1)求点D的坐标;
(2)如图(1),求△ACD的面积;
(3)如图(2),∠OAB与∠OCD的角平分线相交于点M,探求∠AMC的度数并证明你的结论.
相关试题

