【题目】如图,边长相等的两个正方形ABCD和OEFG,若将正方形OEFG绕点O按逆时针方向旋转150°,两个正方形的重叠部分四边形OMCN的面积( )

A. 不变 B. 先增大再减小 C. 先减小再增大 D. 不断增大
参考答案:
【答案】A
【解析】
根据正方形性质得出∠BOC=∠EOG=90°,∠OBC=∠OCD=45°,OB=OC,求出∠BOM=∠CON,根据ASA证△BOM≌△CON,推出两个正方形的重叠部分四边形OMCN的面积等于S△BOC=![]() S正方形ABCD,即可得出选项.
S正方形ABCD,即可得出选项.
∵四边形ABCD、四边形OEFG是两个边长相等正方形,
∴∠BOC=∠EOG=90°,∠OBC=∠OCD=45°,OB=OC,
∴∠BOC-∠COM=∠EOG-∠COM,
即∠BOM=∠CON,
∵在△BOM和△CON中
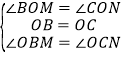 ,
,
∴△BOM≌△CON,
∴两个正方形的重叠部分四边形OMCN的面积是
S△COM+S△CNO=S△COM+S△BOM=S△BOC=![]() S正方形ABCD,
S正方形ABCD,
即不论旋转多少度,阴影部分的面积都等于![]() S正方形ABCD,
S正方形ABCD,
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年3月27日是全国中小学安全教育日,为了让学生了解安全知识,增强安全意识,某校举行了一次“安全知识竞赛”.为了了解这次竞赛的成绩情况,从中抽取了部分学生的成绩为样本,绘制了下列两幅统计图(说明:A级:90~100分;B级:75~89分;C级:60~74分;D级:60分以下).请结合图中提供的信息,解答下列问题:
(1)本次调查共抽取了多少名学生?
(2)扇形统计图中C级所在的扇形的圆心角度数是______;
(3)请把条形统计图补充完整;
(4)若该校共有2000名学生,请你估计安全知识竞赛中A级和B级的学生一共有多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一种夹克和衬衣,夹克每件定价100元,衬衣每件定价50元,商场在开展促销活动期间,向顾客提供两种优惠方案。
方案一:买一件夹克送一件衬衣
方案二:夹克和衬衣均按定价的80%付款
现有顾客要到该商场购买夹克30件,衬衣x件(x>30)
(1)若用方案一购买夹克需付款 元,衬衣需付款(用含x的式子表示) 元,共需付款 元。
若用方案二购买夹克需付款 元,衬衣需付款(用含x的式子表示) 元,共需付款 元。
(2)通过计算说明,购买衬衣多少件时,两种方案付款一样多?
(3)当x=40时,哪种方案更省钱?请说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)如图,在△ABC中,AC=BC,∠ACB=90°,直线l过点C,分别过A、B两点作AD⊥l于点D,作BE⊥l于点E.求证:DE=AD+BE.

(2)如图,已知Rt△ABC,∠C=90°.用尺规作图法作出△ABC的角平分线AD;(不写作法,保留作图痕迹)

(3)若AB=10,CD=3,求△ABD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,BC>AD,∠B与∠C互余, 将AB,CD分别平移到EF和EG的位置,则△EFG为________三角形,若AD=2cm,BC=8cm,则FG=____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC、△ADE均为是顶角为42的等腰三角形,BC和DE分别是底边,图中△_________与△___________,可以通过以点________为旋转中心,旋转角度为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=﹣
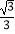 x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限内作等边△ABC.
x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限内作等边△ABC.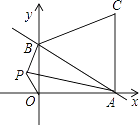
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(a, ),请用含a的式子表示四边形ABPO的面积,并求出当△ABP的面积与△ABC的面积相等时a的值.
),请用含a的式子表示四边形ABPO的面积,并求出当△ABP的面积与△ABC的面积相等时a的值.
相关试题

