【题目】(本题6分)如图,已知△ABC,∠C=Rt∠,AC<BC,D为BC上一点,且到A,B两点的距离相等.

(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B=37°,求∠CAD的度数.
参考答案:
【答案】(1)点D的位置如图所示(D为AB中垂线与BC的交点).(2)16°.
【解析】
试题(1)根据到线段两个端点的距离相等的点在这条线段的垂直平分线上,作出AB的中垂线.(2)要求∠CAD的度数,只需求出∠CAD,而由(1)可知:∠CAD=2∠B
解:(1)点D的位置如图所示(D为AB中垂线与BC的交点).
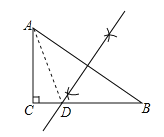
(2)∵在Rt△ABC中,∠B=37°,∴∠CAB=53°.
又∵AD=BD,∴∠BAD=∠B=37°.
∴∠CAD=53°—37°=16°.
故答案为:(1)点D的位置如图所示(D为AB中垂线与BC的交点);(2)16°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将在Rt△ABC绕其锐角顶点A旋转90°得到在Rt△ADE,连接BE,延长DE、BC相交于点F,则有∠BFE=90°,且四边形ACFD是一个正方形.
(1)判断△ABE的形状,并证明你的结论;
(2)用含b代数式表示四边形ABFE的面积;
(3)求证:a2+b2=c2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料,并解决问题:
(1)如图(1),等边△ABC内有一点P若点P到顶点A,B,C的距离分别为3,4,5欲求∠APB的度数,由于PA,PB不在一个三角形中,为了解决本题我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌△ABP这样,就可以利用全等三角形知识,将三条线段的长度转化到一个三角形中从而求出∠APB的度数.
请将下列解题过程补充完整。
∵△ACP′≌△ABP,
∴AP′= =3,CP′= =4,∠ =∠APB.
由题意知旋转角∠PA P′=60°,∴△AP P′为 三角形,
P P′=AP=3,∠A P′P=60°。
易证△P P′C为直角三角形,且∠P P′C=90°,
∴∠APB=∠AP′C=∠A P′P+∠P P′C= °+ °= °.
请你利用第(1)题的解答思想方法,解答下面问题:
已知如图(2),△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,
求证:EF2=BE2+FC2.

-
科目: 来源: 题型:
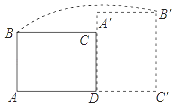
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D′,则点B经过的路径与BA,AC′,C′B′所围成封闭图形的面积是多少?(结果保留π).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的三个顶点在边长为1的正方形网格中,已知A(﹣1,﹣1),B(4,﹣1),C(3,1).
(1)画出△ABC关于y轴对称的△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);
(2)分别写出A′,B′,C′三点的坐标;
(3)请写出所有以AB为边且与△ABC全等的三角形的第三个顶点(不与C重合)的坐标 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求证:△CEF是等腰三角形;
(2)若CD=2,求DF的长.

-
科目: 来源: 题型:
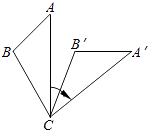
查看答案和解析>>【题目】如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°,∠B′=110°,则∠BCA′的度数是( )
A.90°
B.80°
C.50°
D.30°
相关试题

