【题目】如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边△CDE,使点E、A在直线DC的同侧,连接AE,判断AE与BC的位置关系,并说明理由.

参考答案:
【答案】AE∥BC,理由见解析.
【解析】
试题分析:根据等边三角形性质推出BC=AC,CD=CE,∠BCA=∠ECD=60°,求出∠BCD=∠ACE,根据SAS证△ACE≌△BCD,推出∠EAC=∠DBC=∠ACB,根据平行线的判定推出即可.
证明:∵△ABC和△DEC是等边三角形,
∴BC=AC,CD=CE,∠BCA=∠ECD=60°,∠B=60°,
∴∠BCA﹣∠DCA=∠ECD﹣∠DCA,
即∠BCD=∠ACE,
在△ACE和△BCD中,
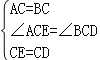 ,
,
∴△ACE≌△BCD(SAS),
∵∠B=60°,
∴∠EAC=∠B=60°,
∵∠ACB=60°,
∴∠EAC=∠ACB,
∴AE∥BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等式(﹣a﹣b)( )=a2﹣b2中,括号里应填的多项式是( )
A. a﹣b B. a+b C. ﹣a﹣b D. b﹣a
-
科目: 来源: 题型:
查看答案和解析>>【题目】若⊙O的半径为5cm,点A到圆心O的距离为4cm,那么点A与⊙O的位置关系是( )
A.点A在圆外 B.点A在圆上
C.点A在圆内 D.不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】绿苑小区在规划设计时,准备在两幢楼房之间,设置一块面积为900平方米的矩形绿地,并且长比宽多10米.设绿地的宽为x米,根据题意,可列方程为( )
A.x(x﹣10)=900
B.x(x+10)=900
C.10(x+10)=900
D.2[x+(x+10)]=900
-
科目: 来源: 题型:
查看答案和解析>>【题目】以点A为顶点作等腰Rt△ABC,等腰Rt△ADE,其中∠BAC=∠DAE=90°,如图1所示放置,使得一直角边重合,连接BD、CE.

(1)试判断BD、CE的数量关系,并说明理由;
(2)延长BD交CE于点F试求∠BFC的度数;
(3)把两个等腰直角三角形按如图2放置,(1)、(2)中的结论是否仍成立?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
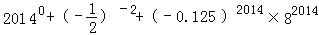
(2)(x+2y)2﹣(3x+y)(x+2y)
(3)[(2a+b)2﹣(2a﹣b)2+6b2]÷2b
(4)[(xy+2)(xy﹣2)﹣2x2y2+4]÷xy,其中x=10,y=﹣
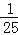 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在某次数学测验中,某小组8名同学的成绩如下:81,73,81,81,85,83,87,89,则这组数据的中位数、众数分别为( ).
A. 80,81 B. 81,89 C. 82,81 D. 73,81
相关试题

