【题目】在平面直角坐标系xOy中,抛物线y=x2+bx+c经过点A(﹣1,t),B(3,t),与y轴交于点C(0,﹣1).一次函数y=x+n的图象经过抛物线的顶点D.
(1)求抛物线的表达式;
(2)求一次函数y=x+n的表达式;
(3)将直线l:y=mx+n绕其与y轴的交点E旋转,使当﹣1≤x≤1时,直线l总位于抛物线的下方,请结合函数图象,求m的取值范围.
参考答案:
【答案】解:(1)二次函数的对称轴是x=![]() =1,
=1,
则﹣![]() =1,
=1,
解得:b=﹣2,
∵抛物线与y轴交于点C(0,﹣1).
∴c=﹣1,
则二次函数的解析式是y=x2﹣2x﹣1;
(2)二次函数y=x2﹣2x﹣1的顶点坐标是(1,﹣2),
代入y=x+n得﹣2=1+n,
解得:n=﹣3,
则一次函数y=x+n的表达式是y=x﹣3;
(3)如图所示: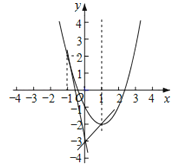
在y=x2﹣2x﹣1中,当x=﹣1时,y=2;
当x=1时,y=﹣2.
当直线y=mx﹣3经过点(﹣1,2)时,﹣m﹣3=2,解得:m=﹣5;
当直线y=mx﹣3经过点(1,﹣2)时,m﹣3=﹣2,解得:m=1.
则当﹣5<m<1时,当﹣1≤x≤1时,直线l总位于抛物线的下方.
【解析】(1)根据A和B对称,可求得对称轴,则b的值即可求得,然后根据函数经过点(0,﹣1),代入即可求得c的值,则抛物线解析式即可求得;
(2)首先求得抛物线的顶点,代入一次函数解析式即可求得n的值,求得一次函数的解析式;
(3)首先求得抛物线上当x=﹣1和x=1时对应点的坐标,然后求得直线y=mx+n经过这两个点时对应的m的值,据此即可求解.
【考点精析】通过灵活运用确定一次函数的表达式,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在“筑梦少年正当时,不忘初心跟党走”知识竟赛中,七年级(2)班2人获一等奖,1人获二等奖,3人获三等奖,奖品价值41元;七年级(7)班1人获一等奖,3人获二等奖,3人获三等奖,奖品价值37元;七年级(13)班5人获二等奖,3人获三等奖,奖品价值_____元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数y=
 +x的图象与性质.
+x的图象与性质.
小东根据学习函数的经验,对函数y= +x的图象与性质进行了探究.
+x的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1)函数y= +x的自变量x的取值范围是;
+x的自变量x的取值范围是;
(2)下表是y与x的几组对应值.
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,3),结合函数的图象,写出该函数的其它性质(一条即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司保安部去商店购买同一品牌的应急灯和手电筒,查看定价后发现,购买一个应急灯和5个手电筒共需50元,购买3个应急灯和2个手电筒共需85元.
(1)求出该品牌应急灯、手电筒的定价分别是多少元?
(2)经商谈,商店给予该公司购买一个该品牌应急灯赠送一个该品牌手电筒的优惠,如果该公司需要手电筒的个数是应急灯个数的2倍还多8个,且该公司购买应急灯和手电筒的总费用不超过670元,那么该公司最多可购买多少个该品牌应急灯?
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面推理过程
如图,已知DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由:

∵DE∥BC(已知)
∴∠ADE= .( )
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF=
 ,
,∠ABE=
 .( )
.( )∴∠ADF=∠ABE
∴DF∥ .( )
∴∠FDE=∠DEB. ( )
-
科目: 来源: 题型:
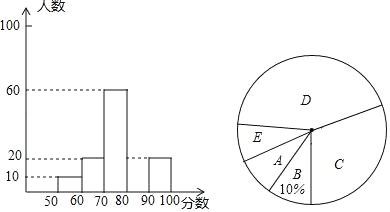
查看答案和解析>>【题目】2018“体彩杯”重庆开州汉丰湖半程马拉松赛开跑前一周,某校七年级数学研究学习小组在某十字路口随机调查部分市民对“半马拉松赛”的了解情况,统计结果后绘制了如图的两副不完整的统计图,请结合图中相关数据回答下列问题:
A
50<n≤60
B
60<n≤70
C
70<n≤80
D
80<n≤90
E
90<n≤100
(1)本次调查的总人数为 人,在扇形统计图中“C”所在扇形的圆心角的度数为 度;
(2)补全频数分布图;
(3)若在这一周里,该路口共有7000人通过,请估计得分超过80的大约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我区某中学体育组因高中教学需要本学期购进篮球和排球共80个,共花费5800元,已知篮球的单价是80元/个,排球的单价是50元/个.
(1)篮球和排球各购进了多少个(列方程组解答)?
(2)因该中学秋季开学准备为初中也购买篮球和排球,教学资源实现共享,体育组提出还需购进同样的篮球和排球共40个,但学校要求花费不能超过2810元,那么篮球最多能购进多少个(列不等式解答)?
相关试题

