【题目】如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2
(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2![]() ,点A的纵坐标为4.
,点A的纵坐标为4.
(1)求该反比例函数和一次函数的解析式;
(2)连接MC,求四边形MBOC的面积.

参考答案:
【答案】(1)反比例函数的解析式为y=![]() ,一次函数的解析式为y=2x+2;(2)4.
,一次函数的解析式为y=2x+2;(2)4.
【解析】
试题分析:(1)根据题意可得B的坐标,从而可求得反比例函数的解析式,进行求得点A的坐标,从而可求得一次函数的解析式;
(2)根据(1)中的函数关系式可以求得点C,点M,点B,点O的坐标,从而可求得四边形MBOC的面积.
试题解析:(1)由题意可得,
BM=OM,OB=2![]() ,
,
∴BM=OM=2,
∴点B的坐标为(﹣2,﹣2),
设反比例函数的解析式为y=![]() ,
,
则﹣2=![]() ,得k=4,
,得k=4,
∴反比例函数的解析式为y=![]() ,
,
∵点A的纵坐标是4,
∴4=![]() ,得x=1,
,得x=1,
∴点A的坐标为(1,4),
∵一次函数y=mx+n(m≠0)的图象过点A(1,4)、点B(﹣2,﹣2),
∴![]() ,得
,得![]() ,
,
即一次函数的解析式为y=2x+2;
(2)∵y=2x+2与y轴交与点C,
∴点C的坐标为(0,2),
∵点B(﹣2,﹣2),点M(﹣2,0),点O(0,0),
∴OM=2,OC=2,MB=2,
∴四边形MBOC的面积是:![]() =4.
=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.

(1)点M、N运动几秒后,M、N两点重合?
(2)点M、N运动几秒后,可得到等边三角形△AMN?
(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形?如存在,请求出此时M、N运动的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下图所示,从2街4巷到4街2巷,走最短的路线,共有几种走法?

-
科目: 来源: 题型:
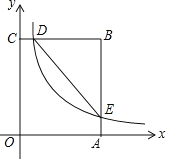
查看答案和解析>>【题目】如图,在矩形OABC中,OA=3,OC=5,分别以OA、OC所在直线为x轴、y轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数y=
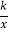 (k>0)的图象经过点D且与边BA交于点E,连接DE.
(k>0)的图象经过点D且与边BA交于点E,连接DE.(1)连接OE,若△EOA的面积为3,则k=___________;
(2)是否存在点D,使得点B关于DE的对称点在OC上?若存在,求出点D的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小颖妈妈的网店加盟了“小神龙”童装销售,有一款童装的进价为60元/件,售价为100元/件,因为刚加盟,为了增加销量,准备对大客户制定如下促销优惠方案:
若一次购买数量超过10件,则每增加一件,所有这一款童装的售价降低1元/件.
例如:一次购买11件时,这11件的售价都为99元/件.请解答下列问题:
(1)一次购买20件这款童装的售价为 元/件,所获利润为 元;
(2)促销优惠方案中,一次购买多少件这款童装,所获利润为625元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线AB与函数y=
 (x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=
(x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD= OC,且△ACD的面积是6,连接BC.
OC,且△ACD的面积是6,连接BC.(1)求m,k,n的值;
(2)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,过O点作EF∥BC,交AB于E,交AC于F.
(1)判断△BEO的形状,并说明理由.
(2)若AB=5cm,AC=4cm,求△AEF的周长.

相关试题

