【题目】阅读下面材料:
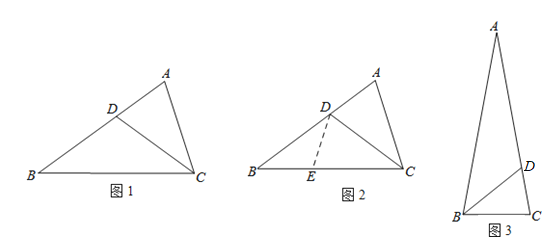
小聪遇到这样一个有关角平分线的问题:如图1,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
小聪思考:因为![]() 平分
平分![]() ,所以可在
,所以可在![]() 边上取点
边上取点![]() ,使
,使![]() ,连接
,连接![]() .这样很容易得到
.这样很容易得到![]() ,经过推理能使问题得到解决(如图2).
,经过推理能使问题得到解决(如图2).
请回答:(1)![]() 是 三角形.
是 三角形.
(2)![]() 的长为 .
的长为 .
参考小聪思考问题的方法,解决问题:
(3)如图3,已知![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,
,![]() .求
.求![]() 的长.
的长.
参考答案:
【答案】(1)等腰;(2)5.8;(3)4.3.
【解析】
(1)由已知条件和辅助线的作法,证得△ACD≌△ECD,得到AD=DE,∠A=∠DEC,由于∠A=2∠B,推出∠DEC=2∠B,等量代换得到∠B=∠EDB,得到△BDE是等腰三角形;
(2)由△BDE是等腰三角形可得BE=DE=AD=2.2,结合EC=AC可得结论;
(3)在BA边上取点E,使BE=BC=2,连接DE,得到△DEB≌△DBC,在DA边上取点F,使DF=DB,连接FE,得到△BDE≌△FDE,即可推出结论.
(1) ![]() 是等腰三角形,
是等腰三角形,
在![]() 与
与![]() 中,
中,
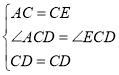 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是等腰三角形;
是等腰三角形;
(2)∵![]() 是等腰三角形,
是等腰三角形,
∴BE=DE,
∵![]() ,
,![]()
∴BC=BE+EC=2.2+3.6=5.8
故![]() 的长为5.8,
的长为5.8,
(3)∵![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
在![]() 边上取点
边上取点![]() ,使
,使![]() ,连接
,连接![]() ,
,
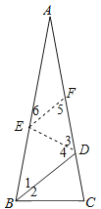
则![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 边上取点
边上取点![]() ,使
,使![]() ,连接
,连接![]() ,
,
则![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+3的图象经过点 (-3,0),(2,-5).
(1)试确定此二次函数的解析式;
(2)请你判断点P(-2,3)是否在这个二次函数的图象上?
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 与
与 有公共顶点
有公共顶点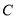 (顶点均按逆时针排列),
(顶点均按逆时针排列),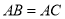 ,
,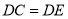 ,
,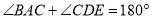 ,
,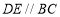 ,点
,点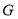 是
是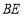 的中点,连接
的中点,连接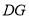 并延长交直线
并延长交直线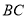 于点
于点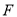 ,连接
,连接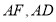 .
.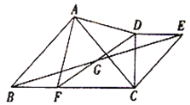
(1)如图,当
 时,
时,求证:①
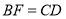 ;
;②
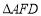 是等腰直角三角形.
是等腰直角三角形.(2)当
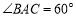 时,画出相应的图形(画一个即可),并直接指出
时,画出相应的图形(画一个即可),并直接指出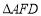 是何种特殊三角形.
是何种特殊三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BC>AB>AC.甲、乙两人想在BC上取一点P,使得∠APC=2∠ABC,其作法如下:
(甲)作AB的中垂线,交BC于P点,则P即为所求;
(乙)以B为圆心,AB长为半径画弧,交BC于P点,则P即为所求.
对于两人的作法,下列判断何者正确?( )

A. 两人皆正确B. 两人皆错误C. 甲正确,乙错误D. 甲错误,乙正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列命题中,写出其逆命题,并判断逆命题的真假.
(1)如果两个角相等,那么它们都是对顶角;
(2)直角都相等;
(3)两条平行线被第三条直线所截,所成的同位角相等;
(4)如果
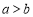 ,那么
,那么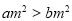 ;
;(5)如果一个三角形是直角三角形,那么它的两个锐角互余.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在等腰直角三角形
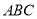 中,
中,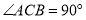 ,
,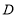 为
为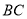 的中点,且
的中点,且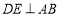 ,垂足为点
,垂足为点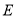 ,过点
,过点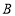 作
作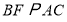 交
交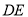 的延长线于点
的延长线于点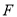 ,联结
,联结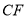 .
.(1)求证:
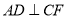 ;
;(2)连接
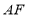 ,试判断
,试判断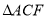 的形状,并说明理由.
的形状,并说明理由.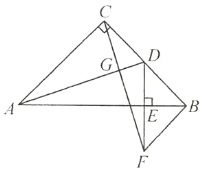
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线AB经过x轴上的点A(2,0),且与抛物线相交于B、C两点,已知B点坐标为(1,1) .
(1)求直线和抛物线的解析式;
(2)如果D为抛物线上一点,使得△AOD与△OBC的面积相等,求D点坐标。

相关试题

