【题目】如图,点A,B分别在x轴、y轴上,点D在第一象限内,DC⊥x轴于点C,AO=DC=2,AB=DA=![]() ,反比例函数y=
,反比例函数y=![]() (k>0)的图象过CD的中点E.
(k>0)的图象过CD的中点E.
(1)求证:△AOB≌△DCA;
(2)求k的值;
(3)△BFG和△DCA关于某点成中心对称,其中点F在y轴上,试判断点G是否在反比例函数的图象上,并说明理由.

参考答案:
【答案】(1)证明见解析(2)3(3)点G(1,3)在反比例函数的图象上
【解析】试题(1)由勾股定理可求出AC的长,从而得到OC的长,可得E坐标,代入即可得;
(2)由△BFG和△DCA关于某点成中心对称可知BF=DC=2,FG=AC=1,从而可得点G坐标,代入判断即可
试题解析:(1)在Rt△ACD中,CD=2,AD=![]() ,
,
∴AC=![]() =1,
=1,
∴OC=OA+AC=2+1=3,
∴D点坐标为(3,2),
∵点E为CD的中点,
∴点E的坐标为(3,1),
∵反比例函数y=![]() (k>0)的图象过点E.
(k>0)的图象过点E.
∴1=![]() ,
,
∴k=3×1=3;
(2)点G在反比例函数的图象上,理由如下:
∵△BFG和△DCA关于某点成中心对称,
∴△BFG≌△DCA,
∴FG=CA=1,BF=DC=2,∠BFG=∠DCA=90°,
而OB=AC=1,
∴OF=OB+BF=1+2=3,
∴G点坐标为(1,3),
∵1×3=3,
∴G(1,3)在反比例函数y=![]() 的图象上.
的图象上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知A(0,5), B(a,b),且a,b满足b=
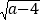 +
+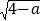 -1.
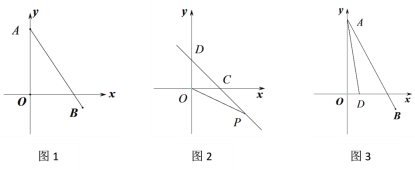
-1.(1)如图,求线段AB的长;
(2)如图,直线CD与x轴、y轴正半轴分别交于点C,D,∠OCD=45°,第四象限的点P(m,n)在直线CD上,且mn=-6,求OP2-OC2的值;
(3)如图,若点D(1,0),求∠DAO +∠BAO的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)四面条的粗细(横截面积)S(mm2)的反比例函数,其图象如图所示.
(1)写出y与S的函数关系式;
(2)求当面条粗1.6 mm2时,面条的总长度是多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃.
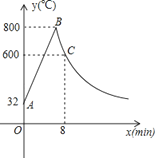
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
-
科目: 来源: 题型:
查看答案和解析>>【题目】蓄电池的电压为定植,使用此电源时,电流I(A)和电阻R(
 )成反比例函数关系,且当I=4A,R=5
)成反比例函数关系,且当I=4A,R=5 .
.(1)蓄电池的电压是多少?请你写出这一函数的表达式.
(2)当电流喂A时,电阻是多少?
(3)当电阻是10
 .时,电流是多少?
.时,电流是多少?(4)如果以此蓄电池为电源的用电器限制电流不超过10A,那么用电器的可变电阻应该控制在什么范围内?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】周末,身高都为1.6米的小芳、小丽来到溪江公园,准备用她们所学的知识测算南塔的高度.如图,小芳站在A处测得她看塔顶的仰角α为45°,小丽站在B处(A、B与塔的轴心共线)测得她看塔顶的仰角β为30°.她们又测出A、B两点的距离为30米.假设她们的眼睛离头顶都为10cm,则可计算出塔高约为(结果精确到0.01,参考数据:
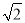 ≈1.414,
≈1.414, 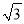 ≈1.732)( )
≈1.732)( )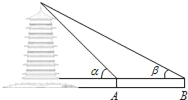
A. 36.21米 B. 37.71米 C. 40.98米 D. 42.48米
相关试题

