【题目】你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)四面条的粗细(横截面积)S(mm2)的反比例函数,其图象如图所示.
(1)写出y与S的函数关系式;
(2)求当面条粗1.6 mm2时,面条的总长度是多少米?
参考答案:
【答案】(1)![]() ;(2)4
;(2)4![]() ;(3)2A;(4)≥2
;(3)2A;(4)≥2![]() .
.
【解析】试题分析:首先根据题意,y与x的关系为乘积一定,为面团的体积,故y与x的关系是反比例函数关系,将数据代入用待定系数法可得反比例函数的关系式;进一步求解可得答案.
解:(1)设y与x的函数关系式为y=![]() ,
,
将x=4,y=32代入上式,
解得:k=4×32=128,
故y=![]() .
.
答:y与x的函数关系式y=![]() .
.
(2)当x=3.2时,y=![]() =40.
=40.
答:当面条粗3.2mm2时,面条的总长度是40米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装厂承揽一项生产夏凉小衫1600件的任务,计划用t天完成.
(1)写出每天生产夏凉小衫w(件)与生产时间t(天)(t>4)之间的函数关系式;
(2)由于气温提前升高,商家与服装厂商议调整计划,决定提前4天交货,那么服装厂每天要多做多少件夏凉小衫才能完成任务?
【答案】(1)
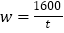 ;(2)
;(2)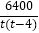
【解析】试题分析:(1)根据实际意义可列出夏凉小衫w(件)与生产时间t(天)(t>4)之间的函数关系式;
(2)根据题意列出t﹣4对应的式子
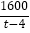 ,与(1)中的式子相减即可.
,与(1)中的式子相减即可.试题解析:(1)由题意可得,函数关系式为:w=
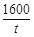 (
( );
);(2)
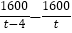 =
=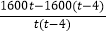 =
=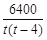 .(或
.(或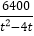 ).
).答:每天多做
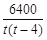 (或
(或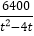 )件夏凉小衫才能完成任务.
)件夏凉小衫才能完成任务.考点:反比例函数的应用.
【题型】解答题
【结束】
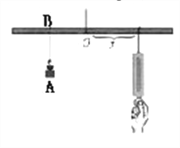
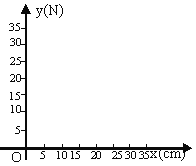
13【题目】如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O右侧用一个弹簧秤向下拉,改变弹簧秤与点O的距离x(cm),观察弹簧秤的示数y(N)的变化情况。实验数据记录如下:
x(cm)
…
10
15
20
25
30
…
y(N)
…
30
20
15
12
10
…
(1)把上表中x,y的各组对应值作为点的坐标,在坐标系中描出相应的点,用平滑曲线连接这些点并观察所得的图象,猜测y(N)与x(cm)之间的函数关系,并求出函数关系式;
(2)当弹簧秤的示数为24N时,弹簧秤与O点的距离是多少cm?
随着弹簧秤与O点的距离不断减小,弹簧秤上的示数将发生怎样的变化?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:在四边形ABFC中,
 =90
=90 的垂直平分线EF交BC于点D,交AB于点E,且CF=AE
的垂直平分线EF交BC于点D,交AB于点E,且CF=AE
(1)试探究,四边形BECF是什么特殊的四边形;
(2)当
 的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.(特别提醒:表示角最好用数字)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知A(0,5), B(a,b),且a,b满足b=
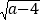 +
+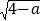 -1.
-1.(1)如图,求线段AB的长;
(2)如图,直线CD与x轴、y轴正半轴分别交于点C,D,∠OCD=45°,第四象限的点P(m,n)在直线CD上,且mn=-6,求OP2-OC2的值;
(3)如图,若点D(1,0),求∠DAO +∠BAO的度数.
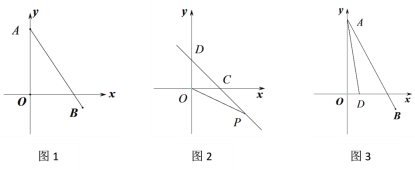
-
科目: 来源: 题型:
查看答案和解析>>【题目】工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃.
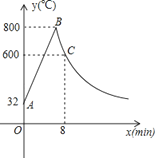
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B分别在x轴、y轴上,点D在第一象限内,DC⊥x轴于点C,AO=DC=2,AB=DA=
 ,反比例函数y=
,反比例函数y= (k>0)的图象过CD的中点E.
(k>0)的图象过CD的中点E.(1)求证:△AOB≌△DCA;
(2)求k的值;
(3)△BFG和△DCA关于某点成中心对称,其中点F在y轴上,试判断点G是否在反比例函数的图象上,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】蓄电池的电压为定植,使用此电源时,电流I(A)和电阻R(
 )成反比例函数关系,且当I=4A,R=5
)成反比例函数关系,且当I=4A,R=5 .
.(1)蓄电池的电压是多少?请你写出这一函数的表达式.
(2)当电流喂A时,电阻是多少?
(3)当电阻是10
 .时,电流是多少?
.时,电流是多少?(4)如果以此蓄电池为电源的用电器限制电流不超过10A,那么用电器的可变电阻应该控制在什么范围内?
相关试题

