【题目】(1)已知: ![]() ,求
,求![]() 的值为_____;
的值为_____;
(2)当式子![]() 有最大值时,最大值是 .
有最大值时,最大值是 .
(3)材料:在学习绝对值时,我们知道了绝对值的几何含义,如|5-3|表示5、3在数轴上对应的两点之间的距离:|5+3|=|5-(-3)|,所以|5+3|表示5、-3在数轴上对应的两点之间的距离:那么![]() 的最小值是
的最小值是
(4)求![]() 的最小值以及取最小值时
的最小值以及取最小值时![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)4;(3)4;(4)x=2
;(2)4;(3)4;(4)x=2
【解析】
(1)根据非负数的性质列式求出x、y的值,然后代入代数式进行计算即可得解;
(2)根据![]() 的非负性即可得解;
的非负性即可得解;
(3))|x+1|+|x-3|的最小值,即x到-1的距离与到3的距离之和最小,从而确定答案;
(4)将|x-3|+|x-2|+|x+1|变形,根据绝对值的几何意义和(3)的结论即可得出结论.
解:(1)
根据题意得,x+y=0,3-y=0,
解得x=-3,y=3,
∴![]() ;
;
(2)∵(x+y)2≥0,
∴(x+y)2=0时,即x=-y时,有最小值0;
∴![]()
![]() 4
4
∴![]() 的最大值是4
的最大值是4
(3)∵|x+1|+|x-3|可表示为x到-1与3两点距离的和,
∴当x在-1与3之间时,|x+1|+|x-3|有最小值|3-(-1)|=4,
(4)∵|x-3|+|x-2|+|x+1|=(|x-3|+|x+1|)+|x-2|,
根据问题(3)可知,要使|x-3|+|x+1|的值最小,x的值只要取-1到3之间(包括-1、3)的任意一个数,
要使|x-2|的值最小,则x=2,
∴当x=2时能同时满足要求,
∴当x=2时![]() 最小,最小值=3+1=4.
最小,最小值=3+1=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“五一”黄金周期间,小明、小亮等同学随家人一同到西安华山游玩,如图是购买门票时,小明与他爸的对话,问题:
(1)小明他们一共去了几个成人?几个学生?
(2)请你帮小明算一算,用哪种方式买票更省钱?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在孝感市关工委组织的“五好小公民”主题教育活动中,我市蓝天学校组织全校学生参加了“红旗飘飘,引我成长”知识竞赛,赛后随机抽取了部分参赛学生的成绩,按从高分到低分将成绩分成
 ,
,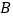 ,
,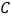 ,
, ,
,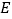 五类,绘制成下面两个不完整的统计图:
五类,绘制成下面两个不完整的统计图: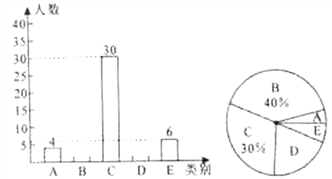
根据上面提供的信息解答下列问题:
(1)
 类所对应的圆心角是________度,样本中成绩的中位数落在________类中,并补全条形统计图;
类所对应的圆心角是________度,样本中成绩的中位数落在________类中,并补全条形统计图;(2)若
 类含有2名男生和2名女生,随机选择2名学生担任校园广播“孝心伴我行”节目主持人,请用列表法或画树状图求恰好抽到1名男生和1名女生的概率.
类含有2名男生和2名女生,随机选择2名学生担任校园广播“孝心伴我行”节目主持人,请用列表法或画树状图求恰好抽到1名男生和1名女生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC底边BC的长为4,面积为12,腰AB的垂直平分线EF交AB于点E,交AC于点F.若D为BC边的中点,M为线段EF上一个动点,则△BDM的周长的最小值为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠MBC和∠NCB是△ABC的外角,点O是∠MBC和∠NCB的平分线的交点,点O叫做△ABC的旁心.

(1)已知∠A=100°,那么∠BOC等于多少度;
(2)猜想∠BOC与∠A有什么数量关系?并证明你的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,
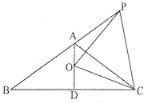
(1)求∠APO+∠DCO的度数;
(2)求证:点P在OC的垂直平分线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,小聪同学利用直尺和圆规完成了如下操作:
,小聪同学利用直尺和圆规完成了如下操作:①作
 的平分线
的平分线 交
交 于点
于点 ;
;②作边
 的垂直平分线
的垂直平分线 ,
, 与
与 相交于点
相交于点 ;
;③连接
 ,
, .
.请你观察图形解答下列问题:

(1)线段
 ,
, ,
,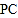 之间的数量关系是________;
之间的数量关系是________;(2)若
 ,求
,求 的度数.
的度数.
相关试题

