【题目】如图,![]() 中,
中,![]() ,小聪同学利用直尺和圆规完成了如下操作:
,小聪同学利用直尺和圆规完成了如下操作:
①作![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ;
;
②作边![]() 的垂直平分线
的垂直平分线![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ;
;
③连接![]() ,
,![]() .
.
请你观察图形解答下列问题:

(1)线段![]() ,
,![]() ,
,![]() 之间的数量关系是________;
之间的数量关系是________;
(2)若![]() ,求
,求![]() 的度数.
的度数.
参考答案:
【答案】(1)![]() ;(2)80°.
;(2)80°.
【解析】(1)根据线段的垂直平分线的性质可得:PA=PB=PC;
(2)根据等腰三角形的性质得:∠ABC=∠ACB=70°,由三角形的内角和得:∠BAC=180°-2×70°=40°,由角平分线定义得:∠BAD=∠CAD=20°,最后利用三角形外角的性质可得结论.
(1)如图,PA=PB=PC,理由是:
∵AB=AC,AM平分∠BAC,
∴AD是BC的垂直平分线,
∴PB=PC,
∵EP是AB的垂直平分线,
∴PA=PB,
∴PA=PB=PC;
故答案为:PA=PB=PC;
(2)∵AB=AC,
∴∠ABC=∠ACB=70°,
∴∠BAC=180°-2×70°=40°,
∵AM平分∠BAC,
∴∠BAD=∠CAD=20°,
∵PA=PB=PC,
∴∠ABP=∠BAP=∠ACP=20°,
∴∠BPC=∠ABP+∠BAC+∠ACP=20°+40°+20°=80°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知:
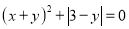 ,求
,求 的值为_____;
的值为_____;(2)当式子
 有最大值时,最大值是 .
有最大值时,最大值是 .(3)材料:在学习绝对值时,我们知道了绝对值的几何含义,如|5-3|表示5、3在数轴上对应的两点之间的距离:|5+3|=|5-(-3)|,所以|5+3|表示5、-3在数轴上对应的两点之间的距离:那么
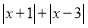 的最小值是
的最小值是 (4)求
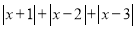 的最小值以及取最小值时
的最小值以及取最小值时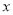 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠MBC和∠NCB是△ABC的外角,点O是∠MBC和∠NCB的平分线的交点,点O叫做△ABC的旁心.

(1)已知∠A=100°,那么∠BOC等于多少度;
(2)猜想∠BOC与∠A有什么数量关系?并证明你的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,
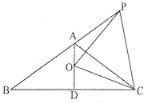
(1)求∠APO+∠DCO的度数;
(2)求证:点P在OC的垂直平分线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从2开始的连续偶数相加,它们和的情况如下表:
加数的个数(n)
和(S)
1
2=1×2
2
2+4=6=2×3
3
2+4+6=12=3×4
4
2+4+6+8=20=4×5
5
2+4+6+8+10=30=5×6
…
…
(1)根据表中的规律,直接写出2+4+6+8+10+12+14=________
(2)根据表中的规律猜想:S=2+4+6+8+…+2n=___________(用n的代数式表示);
(3)利用上题中的公式计算102+104+106+…+200的值(要求写出计算过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,
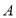 、
、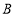 、
、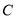 分别为数轴上的三个点,
分别为数轴上的三个点,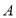 点对应的数为60,
点对应的数为60,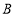 点在
点在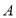 点的左侧,并且与
点的左侧,并且与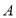 点的距离为30,
点的距离为30,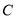 点在
点在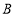 点左侧,
点左侧,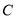 点到
点到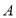 距离是
距离是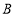 点到
点到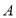 点距离的4倍.
点距离的4倍.
(1)求出数轴上
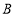 点对应的数及
点对应的数及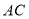 的距离.
的距离.(2)点
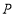 从
从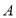 点出发,以3单位/秒的速度项终点
点出发,以3单位/秒的速度项终点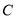 运动,运动时间为
运动,运动时间为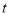 秒.
秒.①点
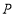 点在
点在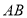 之间运动时,则
之间运动时,则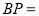 _______.(用含
_______.(用含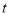 的代数式表示)
的代数式表示)②
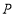 点在
点在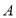 点向
点向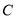 点运动过程中,何时
点运动过程中,何时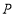 、
、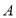 、
、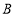 三点中其中一个点是另外两个点的中点?求出相应的时间
三点中其中一个点是另外两个点的中点?求出相应的时间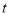 .
.③当
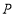 点运动到
点运动到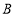 点时,另一点
点时,另一点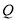 以5单位/秒速度从
以5单位/秒速度从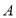 点出发,也向
点出发,也向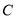 点运动,点
点运动,点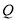 到达
到达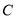 点后立即原速返回到
点后立即原速返回到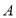 点,那么
点,那么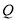 点在往返过程中与
点在往返过程中与 点相遇几次?直接写出相遇是
点相遇几次?直接写出相遇是 点在数轴上对应的数.
点在数轴上对应的数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,Rt△BAP中,∠BAP=90°,已知∠CBO=∠ABP,BP交AC于点O,E为AC上一点,且AE=OC.
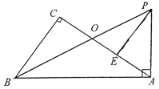
(1)求证:AP=AO;
(2)求证:PE⊥AO.
相关试题

