Question

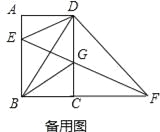
【题目】如图，在矩形ABCD中，BC=1，∠CBD=60°，点E是AB边上一动点（不与点A，B重合），连接DE，过点D作DF⊥DE交BC的延长线于点F，连接EF交CD于点G．

（1）求证：△ADE∽△CDF；

（2）求∠DEF的度数；

（3）设BE的长为x，△BEF的面积为y．

①求y关于x的函数关系式，并求出当x为何值时，y有最大值；

②当y为最大值时，连接BG，请判断此时四边形BGDE的形状，并说明理由．

Answer 1

【答案】（1）证明见解析；

（2）∠DEF=60°；

（3）①y=﹣（x﹣）2+，

∴当x为时，y有最大值；

②四边形BGDE是平行四边形．

【解析】试题分析：（1）根据平行四边形的性质得到∠A=∠ADC=∠DCB=90°，根据余角的性质得到∠ADE=∠CDF，由相似三角形的判定定理即可得到结论；

（2）解直角三角形得到CD=，根据矩形的性质得到AD=BC=1．AB=CD=，根据相似三角形的性质得到=，根据三角函数的定义即可得到结论；

（3）①根据相似三角形的性质得到CF=3﹣x，根据三角形的面积公式得到函数的解析式，根据二次函数的顶点坐标即可得到结论；②根据当x为时，y有最大值，得到BE=，CF=1，BF=2，根据相似三角形的想得到CG=，于是得到BE=DG，由于BE∥DG，即可得到结论．

试题解析：（1）在矩形ABCD中，

∵∠A=∠ADC=∠DCB=90°，

∴∠A=∠DCF=90°，

∵DF⊥DE，

∴∠A=∠EDF=90°，

∴∠ADE=∠CDF，

∴△ADE∽△CDF；

（2）∵BC=1，∠DBC=60°，

∴CD=，

在矩形ABCD中，

∵AD=BC=1．AB=CD=，

∵△ADE∽△CDF，

∴，

∵tan∠DEF=，

∴=，

∴∠DEF=60°；

（3）①∵BE=x，

∴AE=﹣x，

∵△ADE∽△CDF，

∴，

∴CF=3﹣x，

∴BF=BC+CF=4﹣x，

∴y=BEBF=x（4﹣x）=﹣x2+2x，

∵y=﹣x2+2x=﹣（x﹣）2+，

∴当x为时，y有最大值；

②y为最大值时，此时四边形BGDE是平行四边形，

∵当x为时，y有最大值，

∴BE=，CF=1，BF=2，

∵CG∥BE，

∴△CFG∽△BFE，

∴，

∴CG=，

∴DG=，

∴BE=DG，∵BE∥DG，

∴四边形BGDE是平行四边形．