【题目】数学复习课上,张老师出示了下框中的问题:
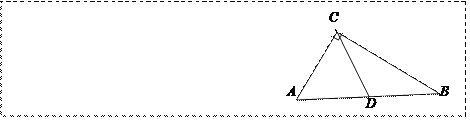
已知:在Rt△ACB中,∠C=90°,点D是斜边AB上的中点,连接CD.
求证:CD=![]() AB.
AB.
问题思考
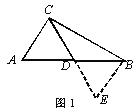
(1)经过独立思考,同学们想出了多种正确的证明思想,其中有位同学的思路如下:如图1,过点B作BE∥AC交CD的延长线于点E。请你根据这位同学的思路提示证明上述框中的问题.
方法迁移
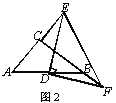
(2)如图2,在Rt△ACB中,∠ACB=90°,点D为AB的中点,点E是线段AC上一动点,连接DE,线段DF始终与DE垂直且交BC于点F。试猜想线段AE,EF,BF之间的数量关系,并加以证明.
拓展延伸
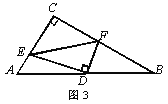
(3)如图3,在Rt△ACB中,∠ACB=90°,点D为AB的中点,点E是线段AC延长线上一动点,连接DE,线段DF始终与DE垂直且交CB延长线于点F。试问第(2)小题中线段AE,EF,BF之间的数量关系会发生改变吗?若会,请写出关系式;若不会,请说明理由.
参考答案:
【答案】(1)CD=![]() AB;(2)AE2+BF2=EF2;(3)线段AE、EF、FB的数量关系不会发生改变,仍有AE2+BF2=EF2.
AB;(2)AE2+BF2=EF2;(3)线段AE、EF、FB的数量关系不会发生改变,仍有AE2+BF2=EF2.
【解析】分析:(1)证ΔACD≌ΔBED和△ACB≌△EBC得证;
(2)如图2,过B作BG∥AC交ED延长线于G,连接GF.通过证ΔADE≌ΔBDG和在Rt△BFG中,得到AE2+BF2=EF2.
(3)如图3,过A作AG//BC交FD的延长线于点G,连接EG,类似(2)问,通过证ΔADG≌ΔBDF,将AE、BF、EF移至Rt△AEG中,可得AE2+BF2=EF2.
详解:(1)证明:∵在⊿ABC中,∠C=90°,D是斜边AB中点,
过B作BE//AC交CD延长线于E,
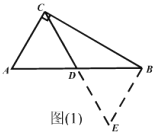
∴∠CAB=∠ABE, ∠ACE=∠BEC,
∴⊿ADC∽⊿BDE,∴D为CE中点,
∵∠CAB+∠CBA=90°,∠ABE+∠CBA=90°,
∴⊿ABC≌⊿ECB,AB=CE,
∴CD=![]() AB.
AB.
(2)证明:过B作BG//AC交ED延长线于G,连接GF.
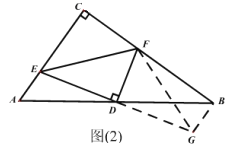
∴∠EAD=∠GBD,又∠EDA=∠GDB,AD=DB,
∴ΔAED≌ΔBDG,∴AE=BG,DE=DG,
又∵DF⊥DE,∴DF是EG中垂线,EF=GF,
∵∠C=90,∠GBF=90,∴BF2+BG2=GF2;
∴AE2+BF2=EF2.
(3)线段AE、EF、FB的数量关系不会发生改变,仍有AE2+BF2=EF2.
证明:如图3,过A作AG//BC交FD的延长线于点G,连接EG,
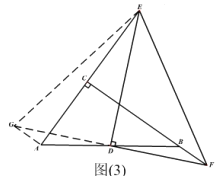
∵AG//BC,∴∠GAD=∠DBF,∠AGD=∠DFB,
∵点D为AB的中点,∴AD=DB,
∴⊿ADG≌⊿BDF,∴AG=BF,GD=DF,
∵DE⊥DF,∴EF=EG,
∵AG//BC,∠EAG=∠ACB=90°,
∴AE2+AG2=EG2,
∴AE2+BF2=EF2.
-
科目: 来源: 题型:
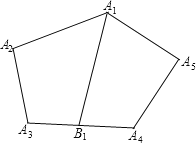
查看答案和解析>>【题目】如图,在五边形A1A2A3A4A5中,B1是A1对边A3A4的中点,连接A1B1,我们称A1B1是这个五边形的一条中对线.如果五边形的每条中对线都将五边形的面积分成相等的两部分.求证:五边形的每条边都有一条对角线和它平行.
-
科目: 来源: 题型:
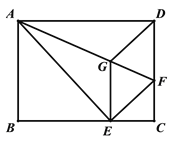
查看答案和解析>>【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)若AG=7、GF=3,求DF的长.
-
科目: 来源: 题型:
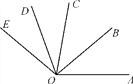
查看答案和解析>>【题目】如图,OB为∠AOC的平分线,OD是∠COE的平分线.
(1)如果∠AOB=40°,∠DOE=30°,那么∠BOD为多少度?
(2)如果∠AOE=140°,∠COD=30°,那么∠AOB为多少度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
 与x轴交于点A,与y轴交于点C.抛物线
与x轴交于点A,与y轴交于点C.抛物线 经过A,C两点,且与x轴交于另一点B(点B在点A右侧).
经过A,C两点,且与x轴交于另一点B(点B在点A右侧).
(1)求抛物线的解析式及点B坐标;
(2)若点M是线段BC上的一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值;
(3)试探究当ME取最大值时,在抛物线上、x轴下方是否存在点P,使以M,F,B,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由.
-
科目: 来源: 题型:
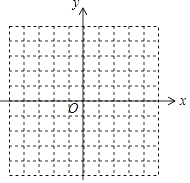
查看答案和解析>>【题目】如图,在所给的平面直角坐标系中描出下列各点:①点A在x轴上方,y轴左侧,距离x轴4个单位长度,距离y轴2个单位长度;②点B在x轴下方,y轴右侧,距离x、y轴都是3个单位长度;③点C在y轴上,位于原点下方,距离原点2个单位长度;④点D在x轴上,位于原点右侧,距离原点4个单位长度. 填空:点A的坐标为________;点B的坐标为________;点B位于第________象限内;点C的坐标为________;点D的坐标为________;线段CD的长度为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在数轴上A点表示数
 ,B点示数
,B点示数 ,C点表示数
,C点表示数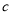 ,
, 是最小的正整数,且
是最小的正整数,且 、
、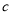 满足
满足 .
.
(1)
 =__________,
=__________, =__________,
=__________,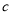 =__________;
=__________;(2)若将数轴折叠,使得A点与C点重合,则点B与数__________表示的点重合;
(3)若点A、点B和点C分别以每秒2个单位、1个单位长度和4个单位长度的速度在数轴上同时向左运动,假设
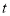 秒钟过后,A、B、C三点中恰有一点为另外两点的中点,求
秒钟过后,A、B、C三点中恰有一点为另外两点的中点,求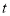 的值;
的值;(4)若点A、点B和点C分别以每秒2个单位、1个单位长度和4个单位长度的速度在数轴上同时向左运动时,小聪同学发现:当点C在B点右侧时,
 BC+3AB的值是个定值,求此时
BC+3AB的值是个定值,求此时 的值.
的值.
相关试题

