搜索
【题目】如图，某人到岛上去探宝，从A处登陆后先往东走4 km，又往北走1.5 km，遇到障碍后又往西走2 km，再折回向北走到4.5 km处往东一拐，仅走0.5 km就找到宝藏．问登陆点A与宝藏埋藏点B之间的距离是多少？
参考答案：
【答案】登陆点A与宝藏埋藏点B之间的距离是6.5 km.
【解析】
过点B作BC⊥AD于点C,根据题意可得AC＝4－2＋0.5＝2.5(km),BC＝4.5＋1.5＝6(km),然后根据勾股定理可得AB2＝AC2＋BC2＝2.52＋62＝6.52,继而求出AB.
解:如图,过点B作BC⊥AD于点C,
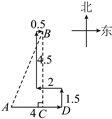
则AC＝4－2＋0.5＝2.5(km),BC＝4.5＋1.5＝6(km),
在Rt△ABC中,由勾股定理,得:
AB2＝AC2＋BC2＝2.52＋62＝6.52,
∴AB＝6.5(km)．
答:登陆点A与宝藏埋藏点B之间的距离是6.5 km.
-
科目： 来源： 题型：
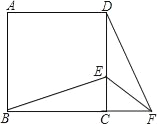
查看答案和解析>>【题目】如图，正方形ABCD中，E为CD边上一点，F为BC延长线上一点，CE=CF．
（1）求证：△BCE≌△DCF；
（2）若∠BEC=60°，求∠EFD的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，OE平分∠AOC，OF平分∠BOC，且∠BOC=60°，若∠AOC+∠EOF=156°，则∠EOF的度数是（ ）
A. 88° B. 30° C. 32° D. 48°
-
科目： 来源： 题型：
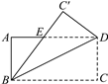
查看答案和解析>>【题目】如图所示，将长方形ABCD沿直线BD折叠，使点C落在点C′处，BC′交AD于点E，AD＝16，AB＝8，求DE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠B＝90°，AB＝7 cm，AC＝25 cm.点P从点A沿AB方向以1 cm/s的速度运动至点B，点Q从点B沿BC方向以6 cm/s的速度运动至点C，P，Q两点同时出发．
(1)求BC的长；
(2)当点P，Q运动2 s时，求P，Q两点之间的距离；
(3)P，Q两点运动几秒时，AP＝CQ?
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，线段
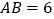cm，点C从点P出发以1cm/s的速度沿AB向左运动，点D从点B出发以2cm/s的速度沿AB向左运动（点C在线段AP上，D在线段BP上）（1）若C，D 运动到任意时刻都有PD=2AC，试说明PB=2AP；
（2）在（1）的条件下，Q是直线AB上一点，若AQ-BQ=PQ，求PQ的值；
（3）在（1）的条件下，若C，D运动了一段时间后恰有AB=2CD，这时点C停止运动，点D继续在线段PB上运动，M，N 分别是CD，PD的中点，求MN的值．
-
科目： 来源： 题型：
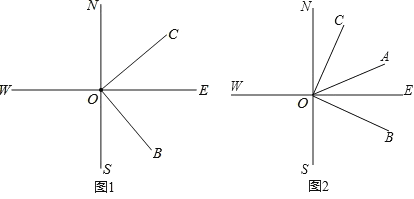
查看答案和解析>>【题目】如图1，直线SN与直线WE相交于点O，射线ON表示正北方向，射线OE表示正东方向，已知射线OB的方向是南偏东m°，射线OC的方向为北偏东n°，且m°的角与n°的角互余．
（1）①若m=60，写出射线OC的方向．（直接回答）
②请直接写出图中所有与∠BOE互余的角及与∠BOE互补的角．
（2）如图2，若射线OA是∠BON的平分线，
①若m=70，求∠AOC的度数．
②若m为任意角度，求∠AOC的度数．（结果用含m的式子表示）
相关试题
