【题目】《孙子算经》是中国古代重要的数学著作,约成书于四、五世纪,也就是大约一千五百年前,传本的《孙子算经》共三卷.卷中有一问题:“今有方物一束,外周一匝有三十二枚,问积几何?”该著作中提出了一种解决此问题的方法:“重置二位,左位减八,余加右位,至尽虚加一,即得.”通过对该题的研究发现,若一束方物外周一匝的枚数n是8的整数倍时,均可采用此方法求解.如图,是解决这类问题的程序框图,若输入n=40,则输出的结果为 . 
参考答案:
【答案】121
【解析】解:模拟程序的运行,可得 n=40,S=40
执行循环体,n=32,S=72
不满足条件n=0,执行循环体,n=24,S=96
不满足条件n=0,执行循环体,n=16,S=112
不满足条件n=0,执行循环体,n=8,S=120
不满足条件n=0,执行循环体,n=0,S=120
满足条件n=0,可得S=121,退出循环,输出S的值为121.
故答案为:121.
模拟程序的运行,依次写出每次循环得到的n,S的值,当n=0时,满足条件退出循环,即可得到输出的S值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ln2(x﹣1)﹣
 ﹣x+3. (Ⅰ)求函数f(x)的单调区间;
﹣x+3. (Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若当x≥1时,不等式(x+1)x+m≤exx+m恒成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(Ⅰ)如果关于x的不等式|x+3|+|x﹣2|<a的解集不是空集,求参数a的取值范围; (Ⅱ)已知正实数a,b,且h=min{a,
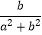 },求证:0<h≤
},求证:0<h≤  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】若对任意的实数a,函数f(x)=(x﹣1)lnx﹣ax+a+b有两个不同的零点,则实数b的取值范围是( )
A.(﹣∞,﹣1]
B.(﹣∞,0)
C.(0,1)
D.(0,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,2b=
 asinB+bcosA,c=4. (Ⅰ)求A;
asinB+bcosA,c=4. (Ⅰ)求A;
(Ⅱ)若D是BC的中点,AD= ,求△ABC的面积.
,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°,E为A1C1的中点,


(Ⅰ)证明:CE⊥平面AB1C1;
(Ⅱ)若AA1= ,∠BAC=30°,求点E到平面AB1C的距离.
,∠BAC=30°,求点E到平面AB1C的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】在“新零售”模式的背景下,某大型零售公司为推广线下分店,计划在S市的A区开设分店.为了确定在该区开设分店的个数,该公司对该市已开设分店的其他区的数据作了初步处理后得到下列表格.记x表示在各区开设分店的个数,y表示这x个分店的年收入之和.
x(个)
2
3
4
5
6
y(百万元)
2.5
3
4
4.5
6
(Ⅰ)该公司已经过初步判断,可用线性回归模型拟合y与x的关系,求y关于x的线性回归方程y=
 ;
;
(Ⅱ)假设该公司在A区获得的总年利润z(单位:百万元)与x,y之间的关系为z=y﹣0.05x2﹣1.4,请结合(Ⅰ)中的线性回归方程,估算该公司应在A区开设多少个分店时,才能使A区平均每个分店的年利润最大?
参考公式: =
=  x+a,
x+a,  =
=  =
=  ,a=
,a=  ﹣
﹣  .
.
相关试题

