搜索
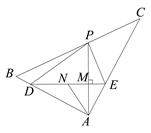
【题目】△ABC中，AB＝6，AC＝8，BC＝10，P为BC边上一动点，过线段AP上的点M作DE⊥AP，交边AB于点D，交边AC于点E，点N为DE中点，若四边形ADPE的面积为18，则AN的最大值=______．
参考答案：
【答案】
【解析】分析：先求APDE=36，再根据直线外一点到直线上任一点的距离，垂线段最短，利用三角形面积公式即可求得AP最短时的长，然后即可求出AN最长时的长.
详解：∵四边形ADPE的面积为18，DE⊥AP，∴
APDE=18,即APDE=36,
在△ABC中，AB=6，AC=8，BC=10，∴∠BAC=90°, ∵点N为DE中点, ∴AN=
DE, ∴DE最大时，AN最大，∵DE=
, ∴AP最小时，DE最大，即AP⊥BC时，AP最小, ∵AP=
,∴DE=
,∴AN=
. 故答案为： 
.
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读：设试验结果落在某个区域S中每一点的机会均等，用A表示事件“试验结果落在S中的一个小区域M中”，那么事件A发生的概率P（A）
.在桌面上放一张50 cm×50 cm的正方形白纸ABCD，⊙O是它的内切圆，小明随机地将1000粒大米撒到该白纸上，其中落在圆内的大米有800粒，由此可得圆周率
的值为（ ）
A.
B. 
C. 
D. 
-
科目： 来源： 题型：
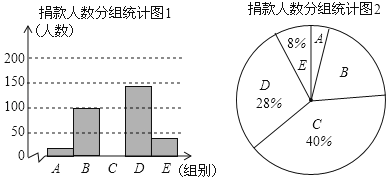
查看答案和解析>>【题目】昆明市某校学生会干部对校学生会倡导的“牵手滇西”自愿捐款活动进行抽样调查，得到一组学生捐款情况的数据，对学校部分捐款人数进行调查和分组统计后，将数据整理成如图所示的统计图（图中信息不完整）．已知A、B两组捐款人数的比为1：5．
组别
捐款额x/元
人数
A
1≤x＜10
a
B
10≤x＜20
100
C
20≤x＜30
D
30≤x＜40
E
40≤x＜50
请结合以上信息解答下列问题．
（1）a＝ ，本次调查样本的容量是 ；
（2）先求出C组的人数，再补全“捐款人数分组统计图1”；
（3）根据统计情况，估计该校参加捐款的4500名学生有多少人捐款在20至40元之间．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在直角梯形ABCD中，动点P从B点出发，沿B→C→D→A匀速运动，设点P运动的路程为x，△ABP的面积为y，图象如图2所示．
（1）在这个变化中，自变量、因变量分别是 、 ；
（2）当点P运动的路程x＝4时，△ABP的面积为y＝ ；
（3）求AB的长和梯形ABCD的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某服装公司招工广告承诺：熟练工人每月工资至少4000元．每天工作8小时，一个月工作25天．月工资底薪1000元，另加计件工资．加工1件A型服装计酬20元，加工1件B型服装计酬15元．在工作中发现一名熟练工加工2件A型服装和3件B型服装需7小时，加工1件A型服装和2件B型服装需4小时．(工人月工资＝底薪+计件工资)
(1)一名熟练工加工1件A型服装和1件B型服装各需要多少小时？
(2)一段时间后，公司规定：“每名工人每月必须加工A，B两种型号的服装，且加工A型服装数量不少于B型服装的一半”．设一名熟练工人每月加工A型服装a件，工资总额为W元．请你运用所学知识判断该公司在执行规定后是否违背了广告承诺？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点A,O,E在同一条直线上,∠BOD= 90°,OD是∠COE的角平分线，找出图中与∠DOE互余的角.甲、乙、丙三个同学的答案如下:
甲:只有一个角，是∠AOB:
乙:有两个角，是∠AOB和∠BOC:
丙:有三个角，是∠AOB,∠BOC,∠COD.
(1)请你判断哪个同学的答案是正确的?
(2)请你说明正确答案的理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，A、B在数轴上对应的数分别用
、
表示，且
.（1）数轴上点A表示的数是 ，点B表示的数是
（2）若一动点P从点A出发，以3个单位长度／秒速度由A向B运动；动点Q从原点O出发，以1个单位长度／秒速度向B运动，点P、Q同时出发，点Q运动到B点时两点同时停止.设点Q运动时间为t秒.
①若P从A到B运动，则P点表示的数为 ,Q点表示的数为 .用含
的式子表示）②当t为何值时，点P与点Q之间的距离为2个单位长度．
相关试题
