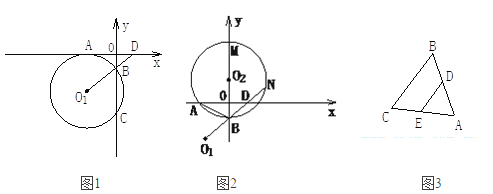
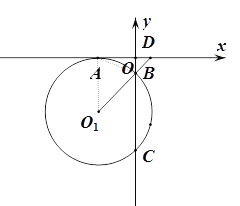
[题目]如图1.平面直角坐标系中.⊙O1与x轴相切于点A(-2.0).与y轴交于B.C两点.O1B的延长线交x轴于点D(.0).连结AB．(1)求证:∠ABO1=∠ABO,(2)设E为优弧的中点.连结AC.BE交于点F.请你探求BE·BF的值．(3)如图2.过A.B两点作⊙O2与y轴的正半轴交于点M.与BD的延长线交于点N.当⊙O2的大小变化时.给出下列两个结论．� 题目和参考答案——青夏教育精英家教网—

【题目】如图1，平面直角坐标系中，⊙O1与x轴相切于点A（-2，0），与y轴交于B、C两点，O1B的延长线交x轴于点D（，0），连结AB．

（1）求证：∠ABO1=∠ABO；

（2）设E为优弧的中点，连结AC、BE交于点F，请你探求BE·BF的值．

（3）如图2，过A、B两点作⊙O2与y轴的正半轴交于点M，与BD的延长线交于点N，当⊙O2的大小变化时，给出下列两个结论．

①BM-BN的值不变；②BM+BN的值不变，其中有且只有一个结论是正确的，请你判断哪一个结论正确，证明正确的结论并求出其值．

（友情提示：如图3，如果DE∥BC，那么）

【答案】（1）证明见解析（2）3（3）BM-BN=BG=2其值不变

【解析】试题分析：（1）连接O1A，AB，由圆O1与x轴切于A，根据切线的性质得到O1A⊥OA，由OB与AO垂直，根据平面内垂直于同一条直线的两直线平行，得到O1A与OB平行，根据两直线平行内错角相等，得到∠O1AB＝∠OBA，再由O1A＝O1B，根据等边对等角可得出∠O1AB＝∠O1BA，等量代换可得出∠ABO1＝∠ABO，得证；

（2）连结CE，根据提示可得，设DB＝2x，则O1D＝5x，∴O1A＝O1B＝5x－2x＝3x，在Rt△DAO1中，利用勾股定理列出方程求出x的值，然后依据切割线定理求出OC、BC，由勾股定理可得AB，然后证△ABF∽△EBC，根据相似三角形的对应边成比例变形即可得出结论；

（3）两个结论中，①BM－BN的值不变正确，理由为：在MB上取一点G，使MG＝BN，连接AM、AN、AG、MN，由∠ABO1为四边形ABMN的外角，根据圆内接四边形的外角等于它的内对角，可得出∠ABO1＝∠NMA，再由∠ABO1＝∠ABO，等量代换可得出∠ABO＝∠NMA，然后利用同弧所对的圆周角相等可得出∠ABO＝∠ANM，等量代换可得出∠NMA＝∠ANM，根据等角对等边可得出AM＝AN，再由同弧所对的圆周角相等，及OM＝BN，利用SAS可得出三角形AMG与三角形ABN全等，根据全等三角形的对应边相等可得出AG＝AB，由AO与BG垂直，根据三线合一得到O为BG的中点，根据OB的长求出BG的长，然后BM－BN＝BM－MG＝BG，由BG为常数得到BM－BN的长不变，得证．

试题解析：

（1）证明：连结O1A，AB，

则O1A⊥OA，

∴O1A∥OB，

∴∠O1AB＝∠ABO，

又∵O1A＝O1B，

∴∠O1AB＝∠O1BA，

∴∠ABO1＝∠ABO；

（2）连结CE，∵O1A∥OB，∴ ，

设DB＝2x，则O1D＝5x，∴O1A＝O1B＝5x－2x＝3x，

在Rt△DAO1中，（3x）2＋（）2＝（5x）2，∴x＝，

∴O1A＝O1B＝，OB＝1，

∵OA是⊙O1的切线，∴OA2＝OB·OC，

∴OC＝4，BC＝3，AB＝，

∵E为优弧AC的中点，∴∠ABF＝∠EBC，

∵∠BAF＝∠E，

∴△ABF∽△EBC，

∴，

∴BE·BF＝AB·BC＝3．

（3）解：①BM－BN的值不变．

证明：在MB上取一点G，使MG＝BN，连结AM、AN、AG、MN，

∵∠ABO1＝∠ABO，∠ABO1＝∠AMN，∠ABO＝∠ANM，

∴∠AMN＝∠ANM，

∴AM＝AN，

∵∠AMG＝∠ANB，MG＝BN，

∴△AMG≌△ANB，

∴AG＝AB，

∵AD⊥BG，

∴BG＝2BO＝2，

∴BM－BN＝BG＝2其值不变．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>