【题目】某一工程,在工程招标时,接到甲、乙两个工程队的投标书.施工一天,需付甲工程队工程款2.4万元,乙工程队工程款1万元.工程领导小组根据甲,乙两队的投标书测算,有如下方案:
(1)甲队单独完成这项工程刚好如期完成;
(2)乙队单独完成这项工程要比规定日期多用12天;
(3)若甲,乙两队合做6天,余下的工程由乙队单独做也正好如期完成.
试问:在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.
参考答案:
【答案】在不耽误工期的前提下,选第三种施工方案最节省工程款.
【解析】
关键描述语为:“甲,乙两队合做3天,余下的工程由乙队单独做也正好如期完成”;说明甲队实际工作了3天,乙队工作了x天完成任务,工作量=工作时间×工作效率等量关系为:甲3天的工作量+乙规定日期的工作量=1列方程.再看费用情况:方案(1)、(3)不耽误工期,符合要求,可以求费用,方案(2)显然不符合要求.
解:设规定日期为x天.由题意得
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
经检验:x=12是原方程的根.
方案(1):2.4×12=28.8(万元);
方案(2)比规定日期多用12天,显然不符合要求;
方案(3):2.4×6+1×12=26.4(万元).
∵28.8>26.4,
∴在不耽误工期的前提下,选第三种施工方案最节省工程款.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
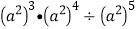
(2)
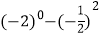 .
.(3)
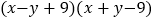 .
. (4)
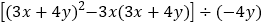 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.

(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:
(1)
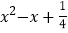 .
. (2)
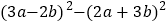 .
.(3)
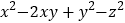 .
. (4)
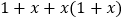 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”
,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”  约为
约为 ,而当手指接触键盘时,肘部形成的“手肘角”
,而当手指接触键盘时,肘部形成的“手肘角”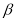 约为
约为 .图
.图 是其侧面简化示意图,其中视线
是其侧面简化示意图,其中视线 水平,且与屏幕
水平,且与屏幕 垂直.
垂直.
(
 )若屏幕上下宽
)若屏幕上下宽 ,科学使用电脑时,求眼睛与屏幕的最短距离
,科学使用电脑时,求眼睛与屏幕的最短距离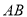 的长.
的长.(
 )若肩膀到水平地面的距离
)若肩膀到水平地面的距离 ,上臂
,上臂 ,下臂
,下臂 水平放置在键盘上,其到地面的距离
水平放置在键盘上,其到地面的距离 ,请判断此时
,请判断此时 是否符合科学要求的
是否符合科学要求的 ?
?(参考数据:
 ,
,  ,
,  ,
,  ,所有结果精确到个位)
,所有结果精确到个位) -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
二次根式的除法,要化去分母中的根号,需将分子、分母同乘以一个恰当的二次根式.
例如:化简
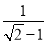 .
.解:将分子、分母同乘以
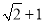 得:
得: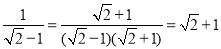 .
.类比应用:
(1)化简:
 ;
;(2)化简:
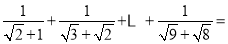 .
.拓展延伸:
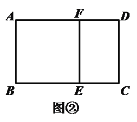
宽与长的比是
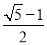 的矩形叫黄金矩形.如图①,已知黄金矩形ABCD的宽AB=1.
的矩形叫黄金矩形.如图①,已知黄金矩形ABCD的宽AB=1.(1)黄金矩形ABCD的长BC= ;
(2)如图②,将图①中的黄金矩形裁剪掉一个以AB为边的正方形ABEF,得到新的矩形DCEF,猜想矩形DCEF是否为黄金矩形,并证明你的结论;

(3)在图②中,连结AE,则点D到线段AE的距离为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,抛物线
 ( a≠0)经过原点,顶点为A(h,k)(h≠0).
( a≠0)经过原点,顶点为A(h,k)(h≠0).(1)当h=1,k=2时,求抛物线的解析式;
(2)若抛物线
 (t≠0)也经过A点,求a与t之间的关系式;
(t≠0)也经过A点,求a与t之间的关系式;(3)当点A在抛物线
 上,且-2≤h<1时,求a的取值范围.
上,且-2≤h<1时,求a的取值范围.
相关试题

