【题目】阅读理解:
二次根式的除法,要化去分母中的根号,需将分子、分母同乘以一个恰当的二次根式.
例如:化简![]() .
.
解:将分子、分母同乘以![]() 得:
得:![]() .
.
类比应用:
(1)化简:![]() ;
;
(2)化简:![]() .
.
拓展延伸:
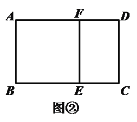
宽与长的比是![]() 的矩形叫黄金矩形.如图①,已知黄金矩形ABCD的宽AB=1.
的矩形叫黄金矩形.如图①,已知黄金矩形ABCD的宽AB=1.
(1)黄金矩形ABCD的长BC= ;
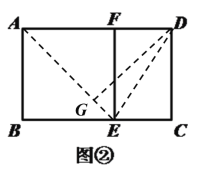
(2)如图②,将图①中的黄金矩形裁剪掉一个以AB为边的正方形ABEF,得到新的矩形DCEF,猜想矩形DCEF是否为黄金矩形,并证明你的结论;

(3)在图②中,连结AE,则点D到线段AE的距离为 .
参考答案:
【答案】类比应用:(1)![]() ;(2)2;拓展延伸:(1)
;(2)2;拓展延伸:(1)![]() ;(2)矩形DCEF为黄金矩形,理由见解析;(3)
;(2)矩形DCEF为黄金矩形,理由见解析;(3)![]()
【解析】
类比应用:
(1)仿照题干中的过程进行计算;
(2)仿照题干中的过程进行计算;
拓展延伸:
(1)根据黄金矩形的定义结合AB=1进行计算;
(2)根据题意算出AD的长,从而得出DF,证明DF和EF的比值为![]() 即可;
即可;
(3)连接AE,DE,过D作DG⊥AE于点G,根据△AED的面积不同算法列出方程,解出DG的长即可.
解:类比应用:
(1)根据题意可得:
![]()
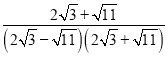 =
=![]() ;
;
(2)根据题意可得:
![]()
=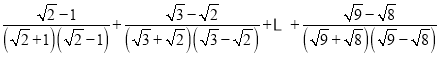
=![]()
=![]()
=2;
拓展延伸:
(1)∵宽与长的比是![]() 的矩形叫黄金矩形,
的矩形叫黄金矩形,
若黄金矩形ABCD的宽AB=1,
则黄金矩形ABCD的长BC=![]() =
=![]() =
=![]() ;
;
(2)矩形DCEF为黄金矩形,理由是:
由裁剪可知:AB=AF=BE=EF=CD=1,
根据黄金矩形的性质可得:AD=BC=![]() ,
,
∴FD=EC=AD-AF=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
故矩形DCEF为黄金矩形;
(3)连接AE,DE,过D作DG⊥AE于点G,
∵AB=EF=1,AD=![]() ,
,
∴AE=![]() ,
,
在△AED中,
S△AED =![]() ,
,
即![]() ,则
,则![]() ,
,
解得DG=![]() ,
,
∴点D到线段AE的距离为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:
(1)
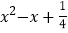 .
. (2)
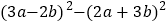 .
.(3)
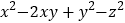 .
. (4)
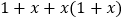 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某一工程,在工程招标时,接到甲、乙两个工程队的投标书.施工一天,需付甲工程队工程款2.4万元,乙工程队工程款1万元.工程领导小组根据甲,乙两队的投标书测算,有如下方案:
(1)甲队单独完成这项工程刚好如期完成;
(2)乙队单独完成这项工程要比规定日期多用12天;
(3)若甲,乙两队合做6天,余下的工程由乙队单独做也正好如期完成.
试问:在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”
,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”  约为
约为 ,而当手指接触键盘时,肘部形成的“手肘角”
,而当手指接触键盘时,肘部形成的“手肘角”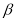 约为
约为 .图
.图 是其侧面简化示意图,其中视线
是其侧面简化示意图,其中视线 水平,且与屏幕
水平,且与屏幕 垂直.
垂直.
(
 )若屏幕上下宽
)若屏幕上下宽 ,科学使用电脑时,求眼睛与屏幕的最短距离
,科学使用电脑时,求眼睛与屏幕的最短距离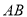 的长.
的长.(
 )若肩膀到水平地面的距离
)若肩膀到水平地面的距离 ,上臂
,上臂 ,下臂
,下臂 水平放置在键盘上,其到地面的距离
水平放置在键盘上,其到地面的距离 ,请判断此时
,请判断此时 是否符合科学要求的
是否符合科学要求的 ?
?(参考数据:
 ,
,  ,
,  ,
,  ,所有结果精确到个位)
,所有结果精确到个位) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,抛物线
 ( a≠0)经过原点,顶点为A(h,k)(h≠0).
( a≠0)经过原点,顶点为A(h,k)(h≠0).(1)当h=1,k=2时,求抛物线的解析式;
(2)若抛物线
 (t≠0)也经过A点,求a与t之间的关系式;
(t≠0)也经过A点,求a与t之间的关系式;(3)当点A在抛物线
 上,且-2≤h<1时,求a的取值范围.
上,且-2≤h<1时,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】把一个含45°角的直角三角板BEF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点B重合,联结DF,点M,N分别为DF,EF的中点,联结MA,MN.
(1)如图1,点E,F分别在正方形的边CB,AB上,请判断MA,MN的数量关系和位置关系,直接
写出结论;
(2)如图2,点E,F分别在正方形的边CB,AB的延长线上,其他条件不变,那么你在(1)中得到的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.
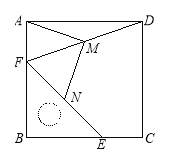
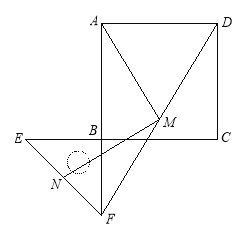
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面内,如图,在平行四边形
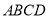 中,
中,  ,
,  ,
,  ,点
,点 为
为 边上任意一点,连接
边上任意一点,连接 ,将
,将 绕点
绕点 逆时针旋转
逆时针旋转 得到线段
得到线段 .
.(
 )当
)当 时,求
时,求 的大小.
的大小.(
 )当
)当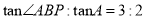 时,求点
时,求点 与点
与点 间的距离(结果保留根号).
间的距离(结果保留根号).(
 )若点
)若点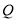 恰好落在平行四边形
恰好落在平行四边形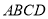 的边所在的条直线上,直接写出
的边所在的条直线上,直接写出 旋转到
旋转到 所扫过的面积(结果保留
所扫过的面积(结果保留 ).
).
相关试题

