【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知:∠BAC=30°,EF⊥AB,垂足为F,连接DF.
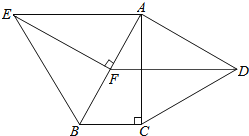
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
参考答案:
【答案】见解析
【解析】
试题分析:(1)首先由Rt△ABC中,由∠BAC=30°可以得到AB=2BC,又由△ABE是等边三角形,EF⊥AB,由此得到AE=2AF,并且AB=2AF,然后证得△AFE≌△BCA,继而证得结论;
(2)根据(1)知道EF=AC,而△ACD是等边三角形,所以EF=AC=AD,并且AD⊥AB,而EF⊥AB,由此得到EF∥AD,再根据平行四边形的判定定理即可证明四边形ADFE是平行四边形.
证明:(1)∵Rt△ABC中,∠BAC=30°,
∴AB=2BC,
又∵△ABE是等边三角形,EF⊥AB,
∴AB=2AF
∴AF=BC,
在Rt△AFE和Rt△BCA中,
![]() ,
,
∴Rt△AFE≌Rt△BCA(HL),
∴AC=EF;
(2)∵△ACD是等边三角形,
∴∠DAC=60°,AC=AD,
∴∠DAB=∠DAC+∠BAC=90°
又∵EF⊥AB,
∴EF∥AD,
∵AC=EF,AC=AD,
∴EF=AD,
∴四边形ADFE是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,把点A(1,﹣5)向上平移3个单位后的坐标是( ).
A. (1,-2)B. (1,-8)C. (4,-5)D. (-2,-5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一张等边三角形纸片沿各边中点剪成4个小三角形,称为第一次操作;然后将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;……,根据以上操作,若要得到100个小三角形,则需要操作的次数是( )
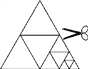
A. 25 B. 33 C. 34 D. 50
-
科目: 来源: 题型:
查看答案和解析>>【题目】特值验证:
当
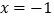 ,0,1,2,5,…时,计算代数式
,0,1,2,5,…时,计算代数式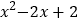 的值,分别得到5,2,1,2,17,….当x的取值发生变化时,代数式
的值,分别得到5,2,1,2,17,….当x的取值发生变化时,代数式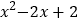 的值却有一个确定的范围,通过多次验证可以发现它的值总大于或等于1,所以1就是它的最小值.
的值却有一个确定的范围,通过多次验证可以发现它的值总大于或等于1,所以1就是它的最小值.变式求证:
我们可以用学过的知识,对
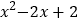 进行恒等变形:
进行恒等变形: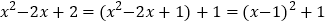 .(注:这种变形方法可称为“配方”)
.(注:这种变形方法可称为“配方”) 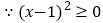 ,
,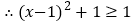 .所以无论x取何值,代数式
.所以无论x取何值,代数式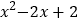 的值不小于1,即最小值为1.
的值不小于1,即最小值为1.迁移实证:
(1)请你用“配方”的方法,确定
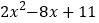 的最小值为3;
的最小值为3;(2)求
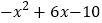 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某农场有A、B两种型号的收割机共20台,每台A型收割机每天可收大麦100亩或者小麦80亩,每台B型收割机每天可收大麦80亩或者小麦60亩,该农场现有19 000亩大麦和11 500亩小麦先后等待收割.先安排这20台收割机全部收割大麦,并且恰好10天时间全部收完.
(1)问A、B两种型号的收割机各多少台?
(2)由于气候影响,要求通过加班方式使每台收割机每天多完成10%的收割量,问这20台收割机能否在一周时间内完成全部小麦收割任务?
-
科目: 来源: 题型:
查看答案和解析>>【题目】你知道为什么任何无限循环小数都可以写成分数形式吗?下面的解答过程会告诉 你原因和方法.
(1)阅读下列材料:
问题:利用一元一次方程将
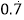 化成分数.
化成分数.设
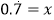 .
.由
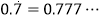 ,可知
,可知 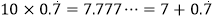 ,
,即
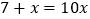 .(请你体会将方程两边都乘以10起到的作用)
.(请你体会将方程两边都乘以10起到的作用)可解得
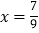 ,即
,即 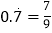 .填空:将
.填空:将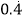 写成分数形式为 .
写成分数形式为 .(2)请仿照上述方法把小数
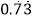 化成分数,要求写出利用一元一次方程进行解答的过程.
化成分数,要求写出利用一元一次方程进行解答的过程. -
科目: 来源: 题型:
查看答案和解析>>【题目】不等式2x-1≤3的解集是( )
A. x≤1B. x≤2C. x≥1D. x≤-2
相关试题

