【题目】如图,AB是圆O的直径,CD是圆O的一条弦,且CD⊥AB于点E. 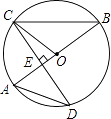
(1)若∠A=48°,求∠OCE的度数;
(2)若CD=4 ![]() ,AE=2,求圆O的半径.
,AE=2,求圆O的半径.
参考答案:
【答案】
(1)解:∵CD⊥AB,∠A=48°,
∴∠ADE=42°.
∴∠AOC=2∠ADE=84°,
∴∠OCE=90°﹣84°=6°
(2)解:因为AB是圆O的直径,且CD⊥AB于点E,所以CE= ![]() CE=
CE= ![]() ×4
×4 ![]() =2
=2 ![]() ,
,
在Rt△OCE中,OC2=CE2+OE2,
设圆O的半径为r,则OC=r,OE=OA﹣AE=r﹣2,所以r2=(2 ![]() )2+(r﹣2)2,
)2+(r﹣2)2,
解得:r=3.所以圆O的半径为3
【解析】(1)首先求出∠ADE的度数,再根据圆周角定理求出∠AOC的度数,最后求出∠OCE的度数;(2)由弦CD与直径AB垂直,利用垂径定理得到E为CD的中点,求出CE的长,在直角三角形OCE中,设圆的半径OC=r,OE=OA﹣AE,表示出OE,利用勾股定理列出关于r的方程,求出方程的解即可得到圆的半径r的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A. 为了了解东北地区初中生每天体育锻炼的时间,应采用普查的方式
B. 平均数相同的甲、乙两组数据,若甲组数据的方差
 ,乙组数据的方差
,乙组数据的方差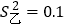 ,则乙组数据比甲组数据稳定
,则乙组数据比甲组数据稳定C. 掷一枚质地均匀的硬币
 次,必有
次,必有 次正面朝上
次正面朝上D. 数据
 ,
, ,
, ,
, ,
,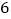 ,
, 的中位数是
的中位数是
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,AD=a,BE∥AC,DE交AC的延长线于F点,交BE于E点.
(1)求证:DF=FE;
(2)若AC=2CF,∠ADC=60°,AC⊥DC,求BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标平面内,二次函数图象的顶点为A(1,﹣4),且过点B(3,0).

(1)求该二次函数的解析式;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店三、四月份出售同一品牌各种规格空调销售台输入下表,回答:
 匹
匹 匹
匹 匹
匹 匹
匹三月




四月




 商店平均每月销售空调________台;
商店平均每月销售空调________台; 商店出售各种规格的空调中,众数有________匹;
商店出售各种规格的空调中,众数有________匹; 在研究六月份进货时,商店经理决定________(匹)的空调要多进,________(匹)的空调要少进.
在研究六月份进货时,商店经理决定________(匹)的空调要多进,________(匹)的空调要少进. -
科目: 来源: 题型:
查看答案和解析>>【题目】随机抽取某城市一年(以
 天计)中的
天计)中的 天日平均气温状况统计如下:
天日平均气温状况统计如下:温度








天数








请根据上述数据填空:
 该组数据的中位数是________
该组数据的中位数是________ ;
; 该城市一年中日平均气温为
该城市一年中日平均气温为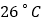 的约有________天;
的约有________天; 若日平均气温在
若日平均气温在 为市民“满意温度”,则该城市一年中达到市民“满意温度”的约有________天.
为市民“满意温度”,则该城市一年中达到市民“满意温度”的约有________天. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC 中,AB=AC,以AB为直径作⊙O,与BC交于点D,过D作AC的垂线,垂足为E.证明:

(1)BD=DC;
(2)DE是⊙O切线.
相关试题

