搜索
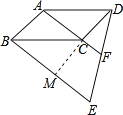
【题目】如图，四边形ABCD为平行四边形，AD=a，BE∥AC，DE交AC的延长线于F点，交BE于E点．
（1）求证：DF=FE；
（2）若AC=2CF，∠ADC=60°，AC⊥DC，求BE的长．
参考答案：
【答案】（1）证明见解析；（2）
【解析】（1）可过点C延长DC交BE于M，可得C，F分别为DM，DE的中点；
（2）在直角三角形ADC中利用勾股定理求解即可.
（1）证明：延长DC交BE于点M，
∵BE∥AC，AB∥DC，
∴四边形ABMC是平行四边形，
∴CM=AB=DC，C为DM的中点，BE∥AC，
则CF为△DME的中位线，
DF=FE；
（2）由（1）得CF是△DME的中位线，故ME=2CF，
又∵AC=2CF，四边形ABMC是平行四边形，
∴AC=ME，
∴BE=2BM=2ME=2AC，
又∵AC⊥DC，
∴在Rt△ADC中利用勾股定理得AC= 
，
∴BE=．
-
科目： 来源： 题型：
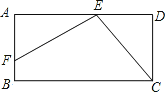
查看答案和解析>>【题目】如图，已知矩形ABCD中，E是AD上一点，F是AB上的一点，EF⊥EC，且EF=EC．
（1）求证：△AEF≌△DCE．
（2）若DE=4cm，矩形ABCD的周长为32cm，求AE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】解答题．
某校学生积极为地震灾区捐款奉献爱心．小颖随机抽查其中30名学生的捐款情况如下：（单位：元）2、5、35、8、5、10、15、20、15、5、45、10、2、8、20、30、40、10、15、15、30、15、8、25、25、30、15、8、10、50．
（1）这30名学生捐款的最大值、最小值、极差、平均数各是多少？
（2）将30名学生捐款额分成下面5组，请你完成频数统计表：
（3）根据上表，作出频数分布直方图．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法中，正确的是（ ）
A. 为了了解东北地区初中生每天体育锻炼的时间，应采用普查的方式
B. 平均数相同的甲、乙两组数据，若甲组数据的方差
，乙组数据的方差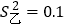
，则乙组数据比甲组数据稳定C. 掷一枚质地均匀的硬币
次，必有
次正面朝上D. 数据
，
，，
，
，
的中位数是
-
科目： 来源： 题型：
查看答案和解析>>【题目】在直角坐标平面内，二次函数图象的顶点为A（1，﹣4），且过点B（3，0）．
（1）求该二次函数的解析式；
（2）将该二次函数图象向右平移几个单位，可使平移后所得图象经过坐标原点？并直接写出平移后所得图象与x轴的另一个交点的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是圆O的直径，CD是圆O的一条弦，且CD⊥AB于点E．
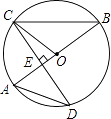
（1）若∠A=48°，求∠OCE的度数；
（2）若CD=4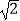
，AE=2，求圆O的半径． -
科目： 来源： 题型：
查看答案和解析>>【题目】某商店三、四月份出售同一品牌各种规格空调销售台输入下表，回答：
匹
匹
匹
匹三月
四月
商店平均每月销售空调________台；
商店出售各种规格的空调中，众数有________匹；
在研究六月份进货时，商店经理决定________（匹）的空调要多进，________（匹）的空调要少进．
相关试题
