【题目】如图,△ABC 中,AB=AC,以AB为直径作⊙O,与BC交于点D,过D作AC的垂线,垂足为E.证明: 
(1)BD=DC;
(2)DE是⊙O切线.
参考答案:
【答案】
(1)证明:如右图所示,
连接AD,
∵AB是直径,
∴∠ADB=90°,
又∵AB=AC,
∴BD=CD
(2)连接OD,
∵∠BAC=2∠BAD,∠BOD=2∠BAD,
∴∠BAC=∠BOD,
∴OD∥AC,
又∵DE⊥AC,
∴∠AED=90°,
∴∠ODB=∠AED=90°,
∴DE是⊙O的切线.
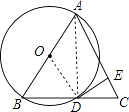
【解析】(1)连接AD,由于AB是直径,那么∠ADB=90°,而AB=AC,根据等腰三角形三线合一定理可知BD=CD;(2)连接OD,由于∠BAC=2∠BAD,∠BOD=2∠BAD,那么∠BAC=∠BOD,可得OD∥AC,而DE⊥AC,易证∠ODB=90°,从而可证DE是⊙O切线.
【考点精析】本题主要考查了圆周角定理和切线的判定定理的相关知识点,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是圆O的直径,CD是圆O的一条弦,且CD⊥AB于点E.
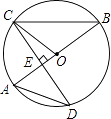
(1)若∠A=48°,求∠OCE的度数;
(2)若CD=4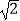 ,AE=2,求圆O的半径.
,AE=2,求圆O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店三、四月份出售同一品牌各种规格空调销售台输入下表,回答:
 匹
匹 匹
匹 匹
匹 匹
匹三月




四月




 商店平均每月销售空调________台;
商店平均每月销售空调________台; 商店出售各种规格的空调中,众数有________匹;
商店出售各种规格的空调中,众数有________匹; 在研究六月份进货时,商店经理决定________(匹)的空调要多进,________(匹)的空调要少进.
在研究六月份进货时,商店经理决定________(匹)的空调要多进,________(匹)的空调要少进. -
科目: 来源: 题型:
查看答案和解析>>【题目】随机抽取某城市一年(以
 天计)中的
天计)中的 天日平均气温状况统计如下:
天日平均气温状况统计如下:温度








天数








请根据上述数据填空:
 该组数据的中位数是________
该组数据的中位数是________ ;
; 该城市一年中日平均气温为
该城市一年中日平均气温为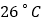 的约有________天;
的约有________天; 若日平均气温在
若日平均气温在 为市民“满意温度”,则该城市一年中达到市民“满意温度”的约有________天.
为市民“满意温度”,则该城市一年中达到市民“满意温度”的约有________天. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,要建一个长方形养鸡场,鸡场的一边靠墙(墙足够长),如果用50m长的篱笆围成中间有一道篱笆墙的养鸡场,设它的长度为x(篱笆墙的厚度忽略不计).

(1)要使鸡场面积最大,鸡场的长度应为多少米?
(2)如果中间有n(n是大于1的整数)道篱笆墙,要使鸡场面积最大,鸡场的长应为多少米?比较(1)(2)的结果,要使鸡场面积最大,鸡场长度与中间隔离墙的道数有怎样的关系? -
科目: 来源: 题型:
查看答案和解析>>【题目】某发电厂共有6台发电机发电,每台的发电量为300万千瓦/月.该厂计划从今年7月开始到年底,对6台发电机各进行一次改造升级.每月改造升级1台,这台发电机当月停机,并于次月再投入发电,每台发电机改造升级后,每月的发电量将比原来提高20%.已知每台发电机改造升级的费用为20万元.将今年7月份作为第1个月开始往后算,该厂第x(x是正整数)个月的发电量设为y(万千瓦).
(1)求该厂第2个月的发电量及今年下半年的总发电量;
(2)求y关于x的函数关系式;
(3)如果每发1千瓦电可以盈利0.04元,那么从第1个月开始,至少要到第几个月,这期间该厂的发电盈利扣除发电机改造升级费用后的盈利总额ω1(万元),将超过同样时间内发电机不作改造升级时的发电盈利总额ω2(万元)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C为线段AB上一点,△ACM,△CBN是等边三角形,直线AN,MC交于点E,直线BM,CN交于点F.
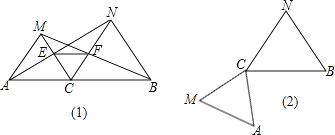
(1)求证:AN=MB;
(2)求证:△CEF为等边三角形;
(3)将△ACM绕点C按逆时针方向旋转90°,其他条件不变,在(2)中画出符合要求的图形,并判断(1)(2)题中的两结论是否依然成立.并说明理由.
相关试题

