【题目】用反证法证明“在同一平面内,若a⊥b,a⊥c,则b∥c时,第一步应假设( )
A.b不平行c
B.a不垂直c
C.a不垂直b
D.b∥c
参考答案:
【答案】A
【解析】解:原命题“在同一平面内,若a⊥b,a⊥c,则b∥c”, 用反证法时应假设结论不成立,
即假设b与c不平行(或b与c相交).
故选:A.
【考点精析】本题主要考查了反证法的相关知识点,需要掌握先假设命题中的结论不成立,然后由此经过推理,引出矛盾,判定所做的假设不正确,从而得到原命题成立,这种证明方法叫做反证法才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次献爱心的捐赠活动中,某班45名同学捐款金额统计如下:
金额(元)
20
30
35
50
100
学生数(人)
5
10
5
15
10
在这次活动中,该班同学捐款金额的众数和中位数分别是( )
A.30,35
B.50,35
C.50,50
D.15,50 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=1是关于x的方程(1-k)x2+k2x-1=0的根,则常数k的值为 ( )
A. 0 B. 1 C. 0或1 D. 0或-1
-
科目: 来源: 题型:
查看答案和解析>>【题目】为解决群众看病贵的问题,有关部门决定降低药价,对某种原价为289元的药品进行连续两次降价后为256元,设平均每次降价的百分率为x,则所列方程是_________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列多项式中不能用平方差公式分解的是( )
A.a2﹣b2B.49x2﹣y2z2
C.﹣x2﹣y2D.16m2n2﹣25p2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学探究课上,老师出示了这样的探究问题,请你一起来探究:已知:C是线段AB所在平面内任意一点,分别以AC、BC为边,在AB同侧作等边△ACE和△BCD,连结AD、BE交于点P.
(1)如图1,当点C在线段AB上移动时,线段AD 与BE的数量关系: .
(2)如图2,当点C在直线AB外,且∠ACB<120°,上面的结论是否还成立?若成立请证明,不成立说明理由.
(3)如图3,在(2)的条件下,以AB为边在AB另一侧作等边三角形△ABF,连结AD、BE和CF交于点P,求证:PB+PC+PA=BE.
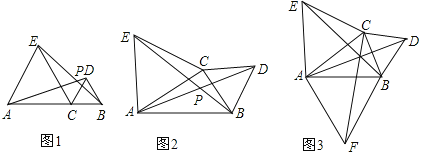
-
科目: 来源: 题型:
查看答案和解析>>【题目】一条船从海岛A出发,以25海里/时的速度向正东方向航行,2小时后到达海岛B处,从A、B望灯塔C,测得∠DBC=68°,∠DAC=34°,求海岛B与灯塔C的距离.

相关试题

