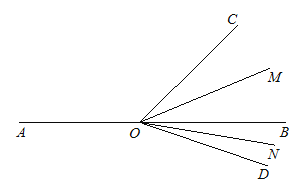
【题目】如图,已知点O为直线AB上一点,射线OC和OD在直线AB的两侧,∠BOC=40°,∠BOD=20°,OM、ON分别平分∠BOC、∠BOD,射线OC以4°/秒的速度绕点O顺时针匀速旋转,射线OD以2°/秒的速度绕点O逆时针匀速旋转.设运动时间为t秒(0<t<100).
(1)运动开始前,∠MON的度数是多少?请写出计算过程.
(2)当t为多少时,∠BOM=8°?请写出计算过程.
(3)当t为多少时,射线OM和射线ON在同一条直线上?请写出计算过程.
参考答案:
【答案】(1)∠MON=30°;(2)t的值为6或14时,∠BOM=8°;(3)t的值为10或70.
【解析】试题分析:(1)由角平分线定义可得:∠MON=![]() ∠COD,由此即可得到结论;
∠COD,由此即可得到结论;
(2)由∠BOM的度数得到∠BOC的度数,解方程40-4t=16或4t-40=16即可得到结论;
(3)分两种情况讨论:①当OM与ON重合时,即OC与OD重合在一起;②当OM与ON互为反向延长线上时.
试题解析:解:(1)∵OM平分∠BOC,∴∠BOM=![]() ∠BOC.
∠BOC.
同理∠BON=![]() ∠BOD,∴∠MON=∠BOM+∠BON=
∠BOD,∴∠MON=∠BOM+∠BON=![]() ∠BOC+
∠BOC+![]() ∠BOD=
∠BOD=![]() ∠COD.
∠COD.
∵∠COD=∠BOC+∠BOD=60°,∴∠MON=30°.
(2)∵∠BOM=![]() ∠BOC=8°,∴∠BOC=16°,∴40-4t=16或4t-40=16,解得t=6或t=14.
∠BOC=8°,∴∠BOC=16°,∴40-4t=16或4t-40=16,解得t=6或t=14.
答:t的值为6或14时,∠BOM=8°.
(3)①当OM与ON重合时,即OC与OD重合在一起,有4t+2t=60, 解得t=10.
②当OM与ON互为反向延长线上时, 有 2t+t=180+30,解得:t=70.
答:t的值为10或70.
-
科目: 来源: 题型:
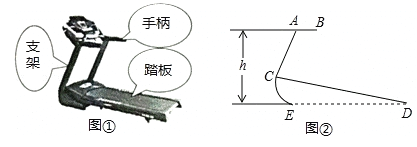
查看答案和解析>>【题目】图①、②分别是某种型号跑步机的实物图与示意图.已知踏板CD长为1.6m,CD与地面DE的夹角∠CDE为12°,支架AC长为0.8m,∠ACD为80°,求跑步机手柄的一端A的高度h(精确到0.1m).
(参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程x2+ax+a-2=0.
(1)求证:不论a为何实数,此方程总有两个不相等的实数根;
(2)设a<0,当二次函数y=x2+ax+a-2的图象与x轴的两个交点的距离为
 时,求出此二次函数的解析式;
时,求出此二次函数的解析式;(3)在(2)的条件下,若此二次函数图象与x轴交于A、B两点,在函数图象上是否存在点P,使得△PAB的面积为
 ,若存在求出P点坐标,若不存在请说明理由.
,若存在求出P点坐标,若不存在请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB和CD的公共部分BD=
 AB=
AB=  CD,线段AB、CD的中点E,F之间距离是10cm,求AB,CD的长.
CD,线段AB、CD的中点E,F之间距离是10cm,求AB,CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中运算正确的是( )
A. 4m-m=3B. xy-2xy=-xyC. 2x+3y=5xyD. a2b-ab2=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点O是直线AB上的一点,
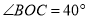 ,OD、OE分别是
,OD、OE分别是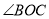 、
、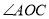 的角平分线.
的角平分线.(1)求
 的度数;
的度数;(2)写出图中与
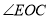 互余的角;
互余的角;(3)图中有
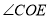 的补角吗?若有,请把它找出来,并说明理由.
的补角吗?若有,请把它找出来,并说明理由.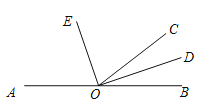
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次夏令营活动中,小霞同学从营地A点出发,要到距离A点10千米的C地去,先沿北偏东70°方向走了8千米到达B地,然后再从B地走了6千米到达目的地C,此时小霞在B地的( )
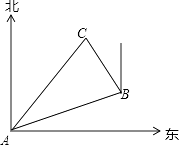
A.北偏东20°方向上
B.北偏西20°方向上
C.北偏西30°方向上
D.北偏西40°方向上
相关试题

