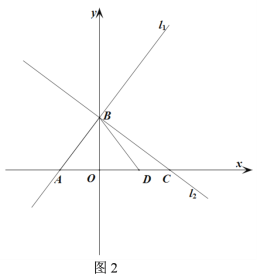
【题目】如图,直线![]() :
:![]() 与x轴、y轴分别交于A、B两点,直线
与x轴、y轴分别交于A、B两点,直线![]() 与x轴、y轴分别交于C、
与x轴、y轴分别交于C、![]() 两点,且
两点,且![]() ︰
︰![]() ︰
︰![]() .
.
(1)求直线![]() 的解析式,并判断
的解析式,并判断![]() 的形状;
的形状;
(2)如图![]() ,
,![]() 为直线
为直线![]() 上一点,横坐标为
上一点,横坐标为![]() ,
,![]() 为直线
为直线![]() 上一动点,当
上一动点,当![]() 最小时,将线段
最小时,将线段![]() 沿射线
沿射线![]() 方向平移,平移后
方向平移,平移后![]() 、
、![]() 的对应点分别为
的对应点分别为![]() 、
、![]() ,当
,当![]() 最小时,求点
最小时,求点![]() 的坐标;
的坐标;
(3)如图![]() ,将
,将![]() 沿着
沿着![]() 轴翻折,得到
轴翻折,得到![]() ,再将
,再将![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() (
(![]() )得到
)得到![]() ,直线
,直线![]() 与直线
与直线![]() 、
、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() .当
.当![]() 为等腰三角形时,请直接写出线段
为等腰三角形时,请直接写出线段![]() 的长.
的长.

参考答案:
【答案】(1)![]() ,
,![]() 为直角三角形 ;(2)
为直角三角形 ;(2)![]() (
(![]() ,
,![]() );(3)
);(3)![]()
![]() ,
,![]()
【解析】
(1)解直角三角形求出AB、AC、BC理由勾股定理的逆定理即可解决问题;
(2)如图1中,作QM⊥x轴于M,首先说明当P、Q、M三点共线,且PM⊥x轴时,PQ+![]() CQ最小,构建一次函数理由方程组确定交点Q的坐标即可;
CQ最小,构建一次函数理由方程组确定交点Q的坐标即可;
(3)分四种情形分别求解即可解决问题;
(1)∵直线![]() :
:![]()
∴![]() (
(![]() ,
,![]() ),
),![]() (
(![]() ,
,![]() )
)
∴在![]() 中,
中,![]()
∵![]() ︰
︰![]() ︰
︰![]()
∴![]()
∴在![]() 中,
中,![]()
即![]() (
(![]() ,
,![]() )
)
设直线![]() :
:![]() (
(![]() )
)
∴![]() 解得
解得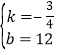
∴直线![]() :
:![]()
∵![]() ,
,![]() ,
,![]()
∴![]()
∴![]() 为直角三角形
为直角三角形
(2)作![]() 轴于
轴于![]() ,则
,则![]() ∽
∽![]()
∴![]()
∴![]() 即
即![]()
∴![]()
∴当![]() 、
、![]() 、
、![]() 三点共线,且
三点共线,且![]() 轴时,
轴时,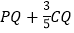 最小
最小
∴![]() (
(![]() ,
,![]() )
)
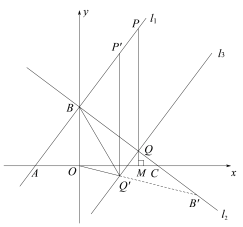
平移过程中,点![]() 在直线
在直线![]() 上移动
上移动
∵![]() 且
且![]() 经过点
经过点![]() (
(![]() ,
,![]() )
)
∴![]() :
:![]()
作点![]() (
(![]() ,
,![]() )关于
)关于![]() 的对称点
的对称点![]() ,则
,则![]() (
(![]() ,
,![]() ),连接
),连接![]() ,与直线
,与直线![]() 的交点即为所求点
的交点即为所求点![]()
∵直线![]() :
:![]()
∴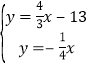 解得
解得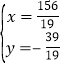
∴![]() (
(![]() ,
,![]() )
)
(3)![]()
![]() ,
,![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数的图象经过点P(2,﹣3).
(1)求该函数的解析式;
(2)若将点P沿x轴负方向平移3个单位,再沿y轴方向平移n(n>0)个单位得到点P′,使点P′恰好在该函数的图象上,求n的值和点P沿y轴平移的方向. -
科目: 来源: 题型:
查看答案和解析>>【题目】一淘宝店主购进
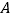 、
、 两款
两款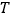 恤在网上进行销售,
恤在网上进行销售,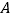 款
款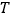 恤每件价格
恤每件价格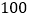 元,
元, 款
款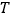 恤每件价格
恤每件价格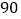 元,第一批共购买
元,第一批共购买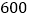 件.
件.(1)该淘宝店主第一批购进的
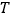 恤的总费用不超过
恤的总费用不超过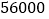 元,求
元,求 款
款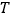 恤最少购买多少件?
恤最少购买多少件?(2)由于销售情况良好,该淘宝店主打算购进第二批
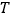 恤,购进的
恤,购进的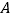 、
、 两款
两款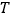 恤件数之比为
恤件数之比为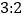 ,价格保持第一批的价格不变;第三批购进
,价格保持第一批的价格不变;第三批购进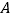 款
款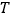 恤的价格在第一批购买的价格上每件减少了
恤的价格在第一批购买的价格上每件减少了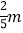 元,
元, 款
款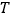 恤的价格比第一批购进的价格上每件增加了
恤的价格比第一批购进的价格上每件增加了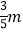 元,
元,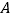 款
款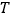 恤的数量比第二批增加了
恤的数量比第二批增加了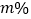 ,
, 款
款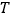 恤的数量比第二批减少了
恤的数量比第二批减少了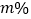 ,第二批与第三批购进的
,第二批与第三批购进的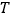 恤的总费用相同,求
恤的总费用相同,求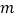 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若正整数k满足个位数字为1,其他数位上的数字均不为1且十位与百位上的数字相等,
我们称这样的数k为“言唯一数”,交换其首位与个位的数字得到一个新数k',并记F(k)=
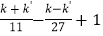 .
.(1)最大的四位“言唯一数”是 ,最小的三位“言唯一数”是 ;
(2)证明:对于任意的四位“言唯一数”m,m+m'能被11整除;
(3)设四位“言唯一数”n=1000x+100y+10y+1(2≤x≤9,0≤y≤9且y≠1,x、y均为整数),若F(n)仍然为“言唯一数”,求所有满足条件的四位“言唯一数”n.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(某进口专营店销售一种“特产”,其成本价是20元/千克,根据以往的销售情况描出销量y(千克/天)与售价x(元/千克)的关系,如图所示.
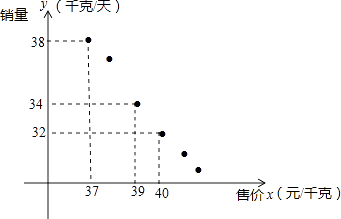
(1)试求出y与x之间的一个函数关系式;
(2)利用(1)的结论:
求每千克售价为多少元时,每天可以获得最大的销售利润.
②进口产品检验、运输等过程需耗时5天,该“特产”最长的保存期为一个月(30天),若售价不低于30元/千克,则一次进货最多只能多少千克? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,补充条件后仍不一定能保证△ABC≌△A′B′C′,则补充的这个条件是( )
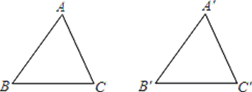
A. BC=B′C′ B. ∠A=∠A′ C. AC=A′C′ D. ∠C=∠C′
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧;平分弧的直径垂直平分这条弧所对的弦.你可以利用这一结论解决问题:
如图,点P在以MN(南北方向)为直径的⊙O上,MN=8,PQ⊥MN交⊙O于点Q,垂足为H,PQ≠MN,弦PC、PD分别交MN于点E、F,且PE=PF.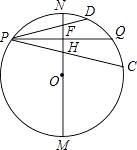
(1)比较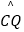 与
与 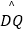 的大小;
的大小;
(2)若OH=2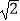 ,求证:OP∥CD;
,求证:OP∥CD;
(3)设直线MN、CD相交所成的锐角为α,试确定cosα=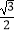 时,点P的位置.
时,点P的位置.
相关试题

