【题目】我们知道:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧;平分弧的直径垂直平分这条弧所对的弦.你可以利用这一结论解决问题:
如图,点P在以MN(南北方向)为直径的⊙O上,MN=8,PQ⊥MN交⊙O于点Q,垂足为H,PQ≠MN,弦PC、PD分别交MN于点E、F,且PE=PF.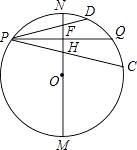
(1)比较 ![]() 与
与 ![]() 的大小;
的大小;
(2)若OH=2 ![]() ,求证:OP∥CD;
,求证:OP∥CD;
(3)设直线MN、CD相交所成的锐角为α,试确定cosα= ![]() 时,点P的位置.
时,点P的位置.
参考答案:
【答案】
(1)解:∵PE=PF,PH⊥EF,
∴PH平分∠FPE,
∴∠DPQ=∠CPQ,
∴ ![]() =
= ![]() ;
;
(2)证明:连结CD、OP、OQ,OQ交CD于B,如图,
∵OH=2 ![]() ,OP=4,
,OP=4,
∴PH= ![]() =2
=2 ![]() ,
,
∴△OPH为等腰直角三角形,
∴∠OPQ=45°,
而OP=OQ,
∴△OPQ为等腰直角三角形,
∴∠POQ=90°,
∴OP⊥OQ,
∵ ![]() =
= ![]() ,
,
∴OQ⊥CD,
∴OP∥CD
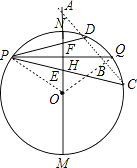
(3)解:直线CD交MN于A,如图,
∵cosα= ![]() ,
,
∴∠α=30°,即直线MN、CD相交所成的锐角为30°,
而OB⊥CD,
∴∠AOB=60°,
∵OH⊥PQ,
∴∠POH=60°,
在Rt△POH中,∵sin∠POH= ![]() ,
,
∴PH=4sin60°=2 ![]() ,
,
即点P到MN的距离为2 ![]() .
.

【解析】(1)根据等腰三角形的性质,由PE=PF,PH⊥EF可判断PH平分∠FPE,然后根据圆中角定理得到 ![]() =
= ![]() ;(2)连结CD、OP、OQ,OQ交CD于B,如图,先计算出PH=2
;(2)连结CD、OP、OQ,OQ交CD于B,如图,先计算出PH=2 ![]() ,则可判断△OPH为等腰直角三角形得到∠OPQ=45°,再判断△OPQ为等腰直角三角形得到∠POQ=90°,然后根据垂径的推理由
,则可判断△OPH为等腰直角三角形得到∠OPQ=45°,再判断△OPQ为等腰直角三角形得到∠POQ=90°,然后根据垂径的推理由 ![]() =
= ![]() 得到OQ⊥CD,则根据平行线的判定方法得OP∥CD;(3)直线CD交MN于A,如图,由特殊角的三角函数值得∠α=30°,即直线MN、CD相交所成的锐角为30°,利用OB⊥CD得到∠AOB=60°,则∠POH=60°,然后在Rt△POH中利用正弦的定义计算出PH即可.本题考查了圆的综合题:熟练掌握垂径定理及其推理、圆周角定理;能够灵活应用等腰直角三角形的性质和三角函数进行几何计算.
得到OQ⊥CD,则根据平行线的判定方法得OP∥CD;(3)直线CD交MN于A,如图,由特殊角的三角函数值得∠α=30°,即直线MN、CD相交所成的锐角为30°,利用OB⊥CD得到∠AOB=60°,则∠POH=60°,然后在Rt△POH中利用正弦的定义计算出PH即可.本题考查了圆的综合题:熟练掌握垂径定理及其推理、圆周角定理;能够灵活应用等腰直角三角形的性质和三角函数进行几何计算.
-
科目: 来源: 题型:
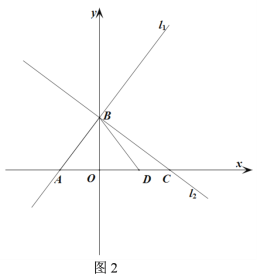
查看答案和解析>>【题目】如图,直线
 :
: 与x轴、y轴分别交于A、B两点,直线
与x轴、y轴分别交于A、B两点,直线 与x轴、y轴分别交于C、
与x轴、y轴分别交于C、 两点,且
两点,且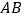 ︰
︰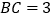 ︰
︰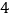 .
.(1)求直线
 的解析式,并判断
的解析式,并判断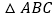 的形状;
的形状;(2)如图
 ,
,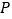 为直线
为直线 上一点,横坐标为
上一点,横坐标为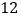 ,
, 为直线
为直线 上一动点,当
上一动点,当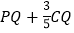 最小时,将线段
最小时,将线段 沿射线
沿射线 方向平移,平移后
方向平移,平移后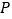 、
、 的对应点分别为
的对应点分别为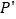 、
、 ,当
,当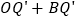 最小时,求点
最小时,求点 的坐标;
的坐标;(3)如图
 ,将
,将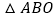 沿着
沿着 轴翻折,得到
轴翻折,得到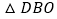 ,再将
,再将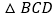 绕着点
绕着点 顺时针旋转
顺时针旋转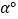 (
( )得到
)得到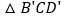 ,直线
,直线 与直线
与直线 、
、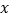 轴分别交于点
轴分别交于点 、
、 .当
.当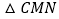 为等腰三角形时,请直接写出线段
为等腰三角形时,请直接写出线段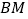 的长.
的长. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】(某进口专营店销售一种“特产”,其成本价是20元/千克,根据以往的销售情况描出销量y(千克/天)与售价x(元/千克)的关系,如图所示.
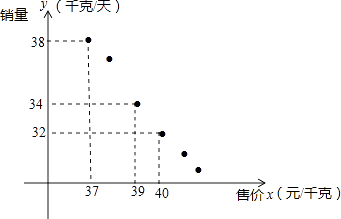
(1)试求出y与x之间的一个函数关系式;
(2)利用(1)的结论:
求每千克售价为多少元时,每天可以获得最大的销售利润.
②进口产品检验、运输等过程需耗时5天,该“特产”最长的保存期为一个月(30天),若售价不低于30元/千克,则一次进货最多只能多少千克? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,补充条件后仍不一定能保证△ABC≌△A′B′C′,则补充的这个条件是( )
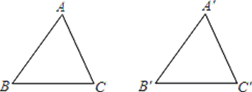
A. BC=B′C′ B. ∠A=∠A′ C. AC=A′C′ D. ∠C=∠C′
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,B、C、D三点在同一条直线上,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
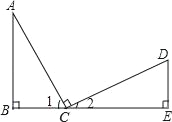
A. ∠A与∠D互为余角 B. ∠A=∠2 C. △ABC≌△ CED D. ∠1=∠2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠A=∠C,点P在边AB上.
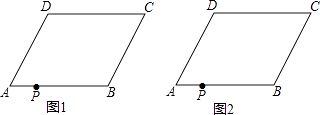
(1)判断四边形ABCD的形状并加以证明;
(2)若AB=AD,以过点P的直线为轴,将四边形ABCD折叠,使点B、C分别落在点B′、C′上,且B′C′经过点D,折痕与四边形的另一交点为Q.
①在图2中作出四边形PB′C′Q(保留作图痕迹,不必说明作法和理由);
②如果∠C=60°,那么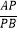 为何值时,B′P⊥AB.
为何值时,B′P⊥AB. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E.某同学分析图形后得出以下结论:①
 BCD≌
BCD≌ CBE;②
CBE;② BAD≌
BAD≌ BCD;③
BCD;③ BDA≌
BDA≌ CEA;④
CEA;④ BOE≌
BOE≌ COD;⑤
COD;⑤  ACE≌
ACE≌ BCE;上述结论一定正确的是
BCE;上述结论一定正确的是
A. ①②③ B. ②③④ C. ①③⑤ D. ①③④
相关试题

