【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于 ![]() 两点,与
两点,与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,其顶点为
,其顶点为![]() .
.
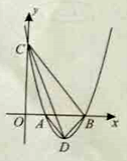
(1)写出![]() 两点的坐标(用含
两点的坐标(用含![]() 的式子表示);
的式子表示);
(2)设![]() ,求
,求![]() 的值;
的值;
(3)当![]() 是直角三角形时,求对应抛物线的解析式.
是直角三角形时,求对应抛物线的解析式.
参考答案:
【答案】(1)C(0,3a),D(2,﹣a);(2)3;(3)y=x2﹣4x+3或y=![]() x2﹣2
x2﹣2![]() x+
x+![]() .
.
【解析】
试题分析:(1)令x=0可求得C点坐标,化为顶点式可求得D点坐标;
(2)令y=0可求得A、B的坐标,结合D点坐标可求得△ABD的面积,设直线CD交x轴于点E,由C、D坐标,利用待定系数法可求得直线CD的解析式,则可求得E点坐标,从而可表示出△BCD的面积,可求得k的值;
(3)由B、C、D的坐标,可表示出BC2、BD2和CD2,分∠CBD=90°和∠CDB=90°两种情况,分别利用勾股定理可得到关于a的方程,可求得a的值,则可求得抛物线的解析式.
试题解析:(1)在y=a(x﹣1)(x﹣3),令x=0可得y=3a,
∴C(0,3a),
∵y=a(x﹣1)(x﹣3)=a(x2﹣4x+3)=a(x﹣2)2﹣a,
∴D(2,﹣a);
(2)在y=a(x﹣1)(x﹣3)中,令y=0可解得x=1或x=3,
∴A(1,0),B(3,0),
∴AB=3﹣1=2,
∴S△ABD=![]() ×2×a=a,
×2×a=a,
如图,设直线CD交x轴于点E,设直线CD解析式为y=kx+b,

把C、D的坐标代入可得![]() ,解得
,解得![]() ,
,
∴直线CD解析式为y=﹣2ax+3a,令y=0可解得x=![]() ,
,
∴E(![]() ,0),
,0),
∴BE=3﹣![]() =
=![]()
∴S△BCD=S△BEC+S△BED=![]() ×
×![]() ×(3a+a)=3a,
×(3a+a)=3a,
∴S△BCD:S△ABD=(3a):a=3,
∴k=3;
(3)∵B(3,0),C(0,3a),D(2,﹣a),
∴BC2=32+(3a)2=9+9a2,CD2=22+(﹣a﹣3a)2=4+16a2,BD2=(3﹣2)2+a2=1+a2,
∵∠BCD<∠BCO<90°,
∴△BCD为直角三角形时,只能有∠CBD=90°或∠CDB=90°两种情况,
①当∠CBD=90°时,则有BC2+BD2=CD2,即9+9a2+1+a2=4+16a2,解得a=﹣1(舍去)或a=1,此时抛物线解析式为y=x2﹣4x+3;
②当∠CDB=90°时,则有CD2+BD2=BC2,即4+16a2+1+a2=9+9a2,解得a=﹣![]() (舍去)或a=
(舍去)或a=![]() ,此时抛物线解析式为y=
,此时抛物线解析式为y=![]() x2﹣2
x2﹣2![]() x+
x+![]() ;
;
综上可知当△BCD是直角三角形时,抛物线的解析式为y=x2﹣4x+3或y=![]() x2﹣2
x2﹣2![]() x+
x+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个三角形的三个内角都不相等,那么最小角一定小于( )
A. 60° B. 59° C. 45° D. 30°
-
科目: 来源: 题型:
查看答案和解析>>【题目】某次篮球联赛初赛阶段,每队有
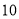 场比赛,每场比赛都要分出胜负,每队胜一场得
场比赛,每场比赛都要分出胜负,每队胜一场得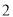 分, 负一场得
分, 负一场得 分,积分超过
分,积分超过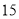 分才能获得参赛资格.
分才能获得参赛资格.(1)已知甲队在初赛阶段的积分为
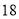 分,求甲队初赛阶段胜、负各多少场;
分,求甲队初赛阶段胜、负各多少场;(2)如果乙队要获得参加决赛资格,那么乙队在初赛阶段至少要胜多少场?
-
科目: 来源: 题型:
查看答案和解析>>【题目】过点(﹣1,7)的直线l与x轴、y轴分别交于点A、B,且与直线y=﹣
 x平行.
x平行.
(1)求直线l的解析式;
(2)写出在线段AB上,横、纵坐标都是整数的点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P在x轴上方,y轴左侧,距x轴2个单位长度,距y轴3个单位长度,则点P的坐标为( )
A.(3,2)B.(-2,-3)C.(-3,2)D.(3,-2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
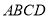 中,
中,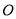 是对角线
是对角线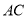 与
与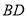 的交点,
的交点, 是
是 边上的动点(点
边上的动点(点 不与
不与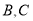 重合),
重合),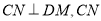 与
与 交于点
交于点 ,连接
,连接 .下列五个结论:①
.下列五个结论:① ;②
;②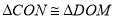 ;③
;③ ;④
;④ ;⑤若
;⑤若 ,则
,则 的最小值是
的最小值是 ,其中正确结论的个数是 ( )
,其中正确结论的个数是 ( )
A.
 B.
B. C.
C.  D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把正方形铁片OABC置于平面直角坐标系中,顶点A的坐标为(3,0),点P(1,2)在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°,第一次旋转至图①位置,第二次旋转至图②位置…,则正方形铁片连续旋转2017次后,点P的坐标为_____________.

相关试题

