【题目】学之道在于悟.希望同学们在问题(1)解决过程中有所悟,再继续探索研究问题(2).
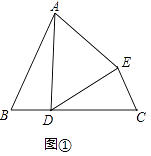
(1)如图①,∠B=∠C,BD=CE,AB=DC. ①求证:△ADE为等腰三角形.
②若∠B=60°,求证:△ADE为等边三角形.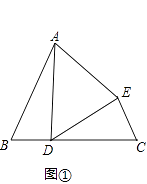
(2)如图②,射线AM与BN,MA⊥AB,NB⊥AB,点P是AB上一点,在射线AM与BN上分别作点C、点 D 满足:△CPD为等腰直角三角形.(要求:利用直尺与圆规,不写作法,保留作图痕迹) 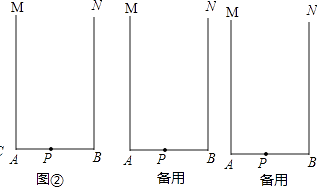
参考答案:
【答案】
(1)解:①证明:∵∠B=∠C,BD=CE,AB=DC,
∴△ABD≌DCE,
∴AB=DC,
∴△ADE为等腰三角形;
②∵△ABD≌△DCE,
∴∠BAD=∠CDE,
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD,
∵∠ADC=∠ADE+∠EDC,
又∵∠BAD=∠CDE.
∴∠ADE=∠B=60°,
∴等腰△ADE为等边三角形.
(2)解:有三种结果,如图所示:
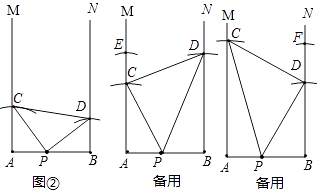
【解析】(1)①先根据∠B=∠C,BD=CE,AB=DC,判定△ABD≌DCE,得出AB=DC,进而得到△ADE为等腰三角形;②根据△ABD≌△DCE,得出∠BAD=∠CDE,再根据∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠EDC,得到∠ADE=∠B=60°,最后判定等腰△ADE为等边三角形;(2)分三种情况讨论:∠CPD为直角顶点;∠PCD是直角顶点;∠PDC是直角顶点,分别进行画图即可.第一种情况:使得AP=BD,BP=AC;第二种情况:使得AC=AB,CE=AP,BD=AE;第三种情况:使得BD=AB,DF=BP,AC=BF.
【考点精析】根据题目的已知条件,利用等腰直角三角形和等腰三角形的判定的相关知识可以得到问题的答案,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点M(a-3,a+1)到x轴的距离是3,且它位于第三象限,求点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列两点中,关于y轴对称的是( )
A. (1,-3)和(-1,3) B. (3,-5)和(-5,3) C. (5,-4)和(5,4) D. (-2,4)和(2,4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果点P(m+3,m-2)在坐标轴上,求m的值和点P的坐标.
-
科目: 来源: 题型:
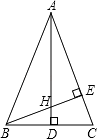
查看答案和解析>>【题目】已知:如图△ABC中,AB=AC,AD和BE是高,它们交于点H,且AE=BE,求证:AH=2BD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一个图形整体沿着某一直线方向移动,会得到一个新的图形,这种移动就叫做_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若两个相似三角形的周长之比为1∶4,则它们的面积之比为( )
A.1∶2B.1∶4C.1∶8D.1∶16
相关试题

