Question

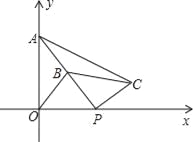
【题目】如图，在平面直角坐标系中，点A的坐标为（0，2），点P（t，0）在x轴上，B是线段PA的中点．将线段PB绕着点P顺时针方向旋转90°，得到线段PC，连结OB、BC．

（1）判断△PBC的形状，并简要说明理由；

（2）当t＞0时，试问：以P、O、B、C为顶点的四边形能否为平行四边形？若能，求出相应的t的值？若不能，请说明理由；

（3）当t为何值时，△AOP与△APC相似？

Answer 1

【答案】（1）等腰直角三角形（2）t=2（3）±1或±4

【解析】试题分析：（1）根据旋转的现在得出PB=PC，再根据B是线段PA的中点，得出∠BPC=90°，从而得出△PBC是等腰直角三角形．

（2）根据∠OBP=∠BPC=90°，得出OB∥PC，再根据B是PA的中点，得出四边形POBC是平行四边形，当OB⊥BP时，得出OP2=2OB2，即t2=2（t2+1），求出符合题意的t的值，即可得出答案；

（3）根据题意得出∠AOP=∠APC=90°，再分两种情况讨论，当时和时，得出△AOP∽△APC和△AOP∽△CPA，分别求出t的值即可．

试题解析：（1）△PBC是等腰直角三角形，理由如下：

∵线段PB绕着点P顺时针方向旋转90°，得到线段PC，

∴PB=PC，

∵B是线段PA的中点，

∴∠BPC=90°，

∴△PBC是等腰直角三角形．

（2）当OB⊥BP时，以P、O、B、C为顶点的四边形为平行四边形．

∵∠OBP=∠BPC=90°，

∴OB∥PC，

∵B是PA的中点，

∴OB=AP=BP=PC，

∴四边形POBC是平行四边形，

当OB⊥BP时，有OP=OB，即OP2=2OB2，

∴t2=2（t2+1），

∴t1=2，t2=﹣2（不合题意），

∴当t=2时，以P、O、B、C为顶点的四边形为平行四边形．

（3）由题意可知，∠AOP=∠APC=90°，

当时，

△AOP∽△APC，

此时OP=OA=1，

∴t=±1，

当时，

△AOP∽△CPA，

此时OP=2OA=4，

∴t=±4，

∴当t=±1或±4时，△AOP与△CPA相似．