【题目】如图,在矩形ABCD内有一点F,FB与FC分别平分∠ABC和∠BCD,点E为矩形ABCD外一点,连接BE,CE.现添加下列条件:①EB∥CF,CE∥BF;②BE=CE,BE=BF;③BE∥CF,CE⊥BE;④BE=CE,CE∥BF,其中能判定四边形BECF是正方形的共有( )

A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】D
【解析】
根据题意可得CF=BF,∠F=90°,根据平行四边形与正方形的的判定即可判断①;根据菱形与正方形的判定即可判断②;根据矩形与正方形的判定即可判断③;根据正方形的判定即可判断.
∵四边形ABCD是矩形,
∴∠DCB=∠ABC=90°,
∵FB与FC分别平分∠ABC和∠BCD,
∴∠FCB=![]() ∠DCB=45°,∠FBC=
∠DCB=45°,∠FBC=![]() ∠ABC=45°,
∠ABC=45°,
∴∠FCB=∠FBC=45°,
∴CF=BF,∠F=180°﹣45°﹣45°=90°,
①∵EB∥CF,CE∥BF,
∴四边形BFCE是平行四边形,
∵CF=BF,∠F=90°,
∴四边形BFCE是正方形,故①正确;
∵BE=CE,BF=BE,CF=BF,
∴BF=CF=CE=BE,
∴四边形BFCE是菱形,
∵∠F=90°,
∴四边形BFCE是正方形,故②正确;
∵BE∥CF,CE⊥BE,
∴CF⊥CE,
∴∠FCE=∠E=∠F=90°,
∴四边形BFCE是矩形,
∵BF=CF,
∴四边形BFCE是正方形,故③正确;
∵CE∥BF,∠FBC=∠FCB=45°,
∴∠ECB=∠FBC=45°,∠EBC=∠FCB=45°,
∵∠F=90°,
∴∠FCE=∠FBE=∠F=90°,
∵BF=CF,
∴四边形BFCE是正方形,故④正确;
即正确的个数是4个.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题

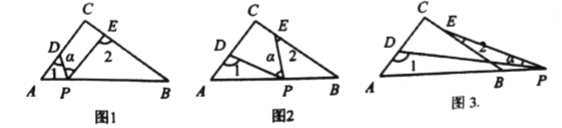
如图1,在△ABC中,AB=AC,射线BP从BA所在位置开始绕点B顺时针旋转,旋转角为α(0°<α<180°)
(1)当∠BAC=60°时,将BP旋转到图2位置,点D在射线BP上.若∠CDP=120°,则∠ACD∠ABD(填“>”、“=”、“<”),线段BD、CD与AD之间的数量关系是;
(2)当∠BAC=120°时,将BP旋转到图3位置,点D在射线BP上,若∠CDP=60°,求证:BD﹣CD= AD;
AD;
(3)将图3中的BP继续旋转,当30°<α<180°时,点D是直线BP上一点(点P不在线段BD上),若∠CDP=120°,请直接写出线段BD、CD与AD之间的数量关系(不必证明). -
科目: 来源: 题型:
查看答案和解析>>【题目】现计划把甲种货物306吨和乙种货物230吨运往某地,已知有A、B两种不同规格的货车共50辆,如果每辆A型货车最多可装甲种货物7吨和乙种货物3吨,每辆B型货车最多可装甲种货物5吨和乙种货物7吨.
(1)装货时如何安排A、B两种货车的辆数,共有哪些方案?
(2)使用A型车每辆费用为600元,使用B型车每辆费用800元,上述方案中,哪个方案运费最省?最省的运费是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8厘米,BC=10厘米,点E在边AB上,且AE=2厘米,如果动点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,动点Q在线段CD上由C点向D点运动,设运动时间为t秒,当△BPE与△CQP全等时,t的值为( )

A. 2B. 1.5或2C. 2.5D. 2或2.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
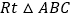 中,
中,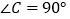 ,点
,点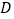 ,
,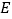 分别是边
分别是边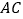 ,
,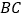 上的点,点
上的点,点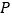 是一动点.记
是一动点.记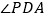 为
为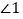 ,
,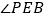 为
为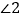 ,
,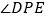 为
为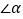 .
.
(1)若点
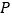 在线段
在线段 上,且
上,且 ,如图1,则
,如图1,则 _____________;
_____________;(2)若点
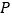 在边
在边 上运动,如图2所示,请猜想
上运动,如图2所示,请猜想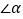 ,
,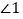 ,
,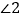 之间的关系,并说明理由;
之间的关系,并说明理由;(3)若点
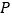 运动到边
运动到边 的延长线上,如图3所示,则
的延长线上,如图3所示,则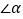 ,
,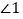 ,
,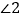 之间又有何关系?请直接写出结论,不用说明理由.
之间又有何关系?请直接写出结论,不用说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=a,DH=4,平移距离CF为a-2,试用a的代数式表示阴影部分的面积____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用锤子以相同的力将铁钉垂直钉入木块,随着铁钉的深入,铁钉所受的阻力也越来越大.当铁钉未进入木块部分长度足够时,每次钉入木块的铁钉长度是前一次的
 ,已知这个铁钉被敲击3次后全部进入木块(木块足够厚),且第一次敲击后,铁钉进入木块的长度是a cm,若铁钉总长度为6cm,则a的取值范围是_______.
,已知这个铁钉被敲击3次后全部进入木块(木块足够厚),且第一次敲击后,铁钉进入木块的长度是a cm,若铁钉总长度为6cm,则a的取值范围是_______.
相关试题

