【题目】如图,已知AC是矩形ABCD的对角线,过AC的中点O的直线EF,交BC于点F,交BC于点F,交AD于点E,连接AF,CE.
(1)求证:△AOE≌△COF;
(2)若EF⊥AC,试判断四边形AFCE是什么特殊四边形?请证明你的结论.

参考答案:
【答案】(1)详见解析;(2)四边形AFCE是菱形,理由见解析.
【解析】
试题分析:(1)求出AO=OC,∠AOE=∠COF,根据平行线得出∠EAO=∠FCO,根据ASA推出两三角形全等即可;(2)根据全等得出OE=OF,推出四边形是平行四边形,再根据EF⊥AC即可推出四边形是菱形;
试题解析:(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EAO=∠FCO,
∵O是AC的中点,
∴AO=CO,
在△AOE和△COF中,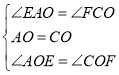 ,
,
∴△AOE≌△COF(ASA);
(2)解:四边形AFCE是菱形;理由如下:
理由是:由(1)△AOE≌△COF得:OE=OF
又∵OA=OC,
∴四边形AFCE是平行四边形,
又∵EF⊥AC
∴平行四边形AFCE是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(3a+2)(4a2-a-1)的结果中二次项系数是( )
A.-3
B.8
C.5
D.-5 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.7a﹣4a=3B.(2a2)3=8a6
C.3a(﹣2a)3=24a4D.a3+2a=2a4
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将直线l1:y=﹣3x﹣1平移后,得到直线l2:y=﹣3x﹣4,则下列平移方式正确的是( )
A.将l1向左平移1个单位B.将l1向右平移1个单位
C.将l1向上平移2个单位D.将l1向上平移1个单位
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.2a2+a2=3a4B.a6÷a2=a3C.a6a2=a12D.(a6)2=a12
-
科目: 来源: 题型:
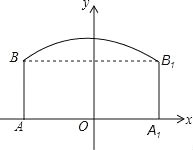
查看答案和解析>>【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长为16m,宽为6m,抛物线的最高点C离地面AA1的距离为8m.
(1)按如图所示的直角坐标系,求表示该抛物线的函数表达式.
(2)一大型汽车装载某大型设备后,高为7m,宽为4m,如果该隧道内设双向行车道,那么这辆贷车能否安全通过?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,∠BAC=90°,AB=AC,BD平分∠ABC.
(1)延长BA到M,使AM=AD,连接CM,求∠ACM的度数.
(2)如图2,若CE⊥BD于E,则BD与EC存在怎样的数量关系?请说明理由.
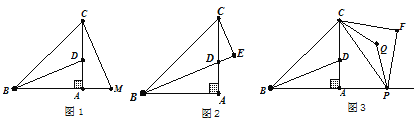
(3)如图3,点P是射线BA上A点右边一动点,以CP为斜边作等腰直角△CPF,其中∠F=90°,点Q为∠FCP与∠CPF的角平分线的交点.当点P运动时,点Q是否一定在射线BD上?若在,请证明;若不在,请说明理由.
相关试题

