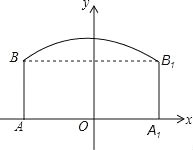
【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长为16m,宽为6m,抛物线的最高点C离地面AA1的距离为8m.
(1)按如图所示的直角坐标系,求表示该抛物线的函数表达式.
(2)一大型汽车装载某大型设备后,高为7m,宽为4m,如果该隧道内设双向行车道,那么这辆贷车能否安全通过?
参考答案:
【答案】(1) y=﹣![]() x2+8;(2)货运卡车能通过,理由见解析.
x2+8;(2)货运卡车能通过,理由见解析.
【解析】
试题分析:(1)根据抛物线在坐标系中的特殊位置,可以设抛物线的解析式为y=ax2+6,再有条件求出a的值即可;(2)隧道内设双行道后,求出纵坐标与7m作比较即可.
试题解析:(1)根据题意得A(﹣8,0),B(﹣8,6),C(0,8),
设抛物线的解析式为y=ax2+8(a≠0),把B(﹣8,6)代入
64a+8=6
解得:a=﹣![]() .
.
抛物线的解析式为y=﹣![]() x2+8.
x2+8.
(2)根据题意,把x=±4代入解析式,
得y=7.5m.
∵7.5m>7m,
∴货运卡车能通过.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将直线l1:y=﹣3x﹣1平移后,得到直线l2:y=﹣3x﹣4,则下列平移方式正确的是( )
A.将l1向左平移1个单位B.将l1向右平移1个单位
C.将l1向上平移2个单位D.将l1向上平移1个单位
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC是矩形ABCD的对角线,过AC的中点O的直线EF,交BC于点F,交BC于点F,交AD于点E,连接AF,CE.
(1)求证:△AOE≌△COF;
(2)若EF⊥AC,试判断四边形AFCE是什么特殊四边形?请证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.2a2+a2=3a4B.a6÷a2=a3C.a6a2=a12D.(a6)2=a12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,∠BAC=90°,AB=AC,BD平分∠ABC.
(1)延长BA到M,使AM=AD,连接CM,求∠ACM的度数.
(2)如图2,若CE⊥BD于E,则BD与EC存在怎样的数量关系?请说明理由.
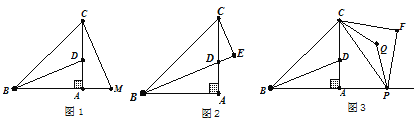
(3)如图3,点P是射线BA上A点右边一动点,以CP为斜边作等腰直角△CPF,其中∠F=90°,点Q为∠FCP与∠CPF的角平分线的交点.当点P运动时,点Q是否一定在射线BD上?若在,请证明;若不在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果∠A=36°18′,那么∠A的补角为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把a2﹣4a多项式分解因式,结果正确的是( )
A. a(a﹣4) B. (a+2)(a﹣2) C. a(a+2)(a﹣2) D. (a﹣2)2﹣4
相关试题

