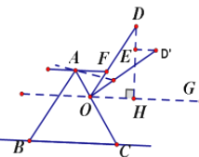
【题目】图 1 是小红在“淘宝双 11”活动中所购买的一张多档位可调节靠椅,档位调节示意图如图 2 所示。已知两支脚 AB=AC,O 为 AC 上固定连接点,靠背 OD=10 分米。档位为Ⅰ档时,OD∥AB,档位为Ⅱ挡时,OD’⊥AC,过点O作OG∥BC,则∠DOG+∠D’OG=_________°当靠椅由Ⅰ档调节为Ⅱ档时,靠背顶端 D 向后靠至 D’,此时点 D 移动的水平距离是 2 分米,即 ED’=2 分米。DH⊥OG于点H,则D到直线OG的距离为_________ 分米.

参考答案:
【答案】90 8
【解析】
先利用平行线的性质与等腰三角形的性质证明∠DOG=∠COG,在利用等量代换计算出∠DOG+∠D’OG=∠COD’=90°;先构造Rt△OMD’,再利用全等的性质以及勾股定理计算DH的长.
(1)过点D’作MD’⊥OH于点M,记AB与OH交于点N
∵OD∥AB,OG∥BC
∴∠DOG=∠ANO,∠ANO=∠ABC,∠ACB=∠COG
∴∠DOG=∠ABC
∵AB=AC
∴∠ABC=∠ACB
∴∠DOG=∠ABC=∠ACB=∠COG
∵OD’⊥AC
∴∠COD’=90°
∴∠DOG+∠D’OG=∠COG+∠D’OG=∠COD’=90°
(2)∵DH⊥OG,D’M⊥OG
∴∠OHD=∠OMD’=90°
∴在Rt△OHD中,∠DOG+∠ODH=90°
又∵∠DOG+∠D’OG=90°
∴∠ODH=∠D’OG
∵旋转
∴OD=D’O
在△ODH和△D’OM中

∴△ODH≌△D’OM(AAS)
∴DH=OM
又∵HM=ED’=2
∴DH=OM=OH+HM=OH+2
不妨设OH=x,则DH=x+2
∴在Rt△OHD中,OD=10,
由勾股定理可得:![]()
即:![]()
解得:![]() ,
,![]() (舍去)
(舍去)
∴D到直线OG的距离为DH=x+2=8.
故答案为:90,8.

-
科目: 来源: 题型:
查看答案和解析>>【题目】《代数学》中记载,形如x2+8x=33的方程,求正数解的几何方法是:“如图1,先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为2x的矩形,得到大正方形的面积为33+16=49,则该方程的正数解为7﹣4=3.”小聪按此方法解关于x的方程x2+10x+m=0时,构造出如图2所示的图形,已知阴影部分的面积为50,则该方程的正数解为( )


A.6B.
 C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一个转盘分成六等份,依次标上数字1、2、3、4、5、6,小明和小芳分别只转动一次转盘.小明同学先转动转盘,结果指针指向2,接下来小芳转动转盘,若把小明和小芳转动转盘指针指向的数字分别记作
 、
、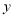 ,把
,把 、
、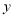 作为点
作为点 的横、纵坐标.
的横、纵坐标.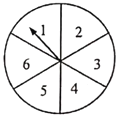
(1)写出点
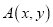 所有可能的坐标;
所有可能的坐标;(2)求点
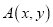 在直线
在直线 上的概率.
上的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图在平行四边形ABCD中,∠ABC=60°,AB=4,四条内角平分线围成四边形EFGH面积为
 ,则平行四边形ABCD面积为________
,则平行四边形ABCD面积为________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一座抛物线型拱桥,已知桥下在正常水位AB时,水面宽8m,水位上升3m, 就达到警戒水位CD,这时水面宽4m,若洪水到来时,水位以每小时0.2m的速度上升,求水过警戒水位后几小时淹到桥拱顶.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某政府部门进行公务员招聘考试,其中三人中录取一人,他们的成绩如下:
人
测试成绩
题目
甲
乙
丙
文化课知识
74
87
69
面试
58
74
70
平时表现
87
43
65
(1)按照平均成绩甲、乙、丙谁应被录取?
(2)若按照文化课知识、面试、平时表现的成绩已4:3:1的比例录取,甲、乙、丙谁应被录取?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售一款口罩,每袋的进价为12元,计划售价大于12元但不超过22元,通过试场调查发现,这种口罩每袋售价提高1元,日均销售量降低5袋,当售价为18元时,日均销售量为50袋.
(1)在售价为18元的基础上,将这种口罩的售价每袋提高x元,则日均销售量是 袋;(用含x的代数式表示)
(2)要想销售这种口罩每天赢利275元,该商场每袋口罩的售价要定为多少元?
相关试题

