【题目】已知:如图,在矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点O,点P从点A出发,沿AD方向匀速运动,速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为1cm/s;当一个点停止运动时,另一个点也停止运动.连接PO并延长,交BC于点E,过点Q作QF∥AC,交BD于点F.设运动时间为t(s)(0<t<6),解答下列问题: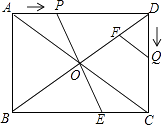
(1)当t为何值时,AP=PO.
(2)设五边形OECQF的面积为S(cm2),试确定S与t的函数关系式;
(3)在运动过程中,是否存在某一时刻t,使OD平分∠COP?若存在,求出t的值;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:∵在矩形ABCD中,AB=6cm,BC=8cm,∠ABC=90°,
∴AC=10,AO= ![]() AC=5,
AC=5,
∵AP=PO=t,
过P作PM⊥AO,如图1所示:

∴AM= ![]() AO=
AO= ![]() ,
,
∵∠PMA=∠ADC=90°,∠PAM=∠CAD,
∴△APM∽△ACD,
∴ ![]() ,即
,即 ![]() ,
,
解得:t= ![]() ,
,
即t= ![]() 时,AP=PO;
时,AP=PO;
(2)
解:过点O作OH⊥BC交BC于点H,则OH= ![]() CD=
CD= ![]() AB=3cm.
AB=3cm.
由矩形的性质可知∠PDO=∠EBO,DO=BO,
在△DOP和△BOE中,  ,
,
∴△DOP≌BOE(ASA),
∴BE=PD=8﹣t,
则S△BOE= ![]() BEOH=
BEOH= ![]() ×3(8﹣t)=12﹣
×3(8﹣t)=12﹣ ![]() t.
t.
∵FQ∥AC,
∴△DFQ∽△DOC,相似比为 ![]() ,
,
∴ ![]() =
= ![]() ,
,
∵S△DOC= ![]() S矩形ABCD=
S矩形ABCD= ![]() ×6×8=12cm2,
×6×8=12cm2,
∴S△DFQ=12× ![]() =
= ![]() ,
,
∴S五边形OECQF=S△DBC﹣S△BOE﹣S△DFQ= ![]() ×6×8﹣(12﹣
×6×8﹣(12﹣ ![]() t)﹣
t)﹣ ![]() =﹣
=﹣ ![]() t2+
t2+ ![]() t+12;
t+12;
∴S与t的函数关系式为S=﹣ ![]() t2+
t2+ ![]() t+12;
t+12;
(3)
解:存在,理由如下:
如图3,过D作DM⊥PE于M,DN⊥AC于N,

∵∠POD=∠COD,
∴DM=DN= ![]() ,
,
∴ON=OM= ![]() =
= ![]() ,
,
∵OPDM=3PD,
∴OP=5﹣ ![]() t,
t,
∴PM= ![]() ﹣
﹣ ![]() t,
t,
∵PD2=PM2+DM2,
∴(8﹣t)2=( ![]() ﹣
﹣ ![]() t)2+(
t)2+( ![]() )2,
)2,
解得:t=16(不合题意,舍去),t= ![]() ,
,
∴当t= ![]() 时,OD平分∠COP.
时,OD平分∠COP.
【解析】(1.)根据矩形的性质和勾股定理得到AC=10,过P作PM⊥AO,证明△APM∽△ACD,根据相似三角形的性质即可得出答案;
(2.)过点O作OH⊥BC交BC于点H,已知BE=PD,则可求△BOE的面积;可证得△DFQ∽△DOC,由相似三角形的面积比可求得△DFQ的面积,从而可求五边形OECQF的面积.
(3.)由角平分线的性质得到DM=DN= ![]() ,根据勾股定理得到ON=OM=
,根据勾股定理得到ON=OM= ![]() =
= ![]() ,由三角形的面积公式得到OP=5﹣
,由三角形的面积公式得到OP=5﹣ ![]() t,根据勾股定理列方程,解方程即可得到结论.
t,根据勾股定理列方程,解方程即可得到结论.
【考点精析】本题主要考查了全等三角形的性质的相关知识点,需要掌握全等三角形的对应边相等; 全等三角形的对应角相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:∠MON=30°,点A1、A2、A3、…在射线ON上,点B1、B2、B3、…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4、…均为等边三角形,若OA1=1,则△A9B9A10的边长为( )
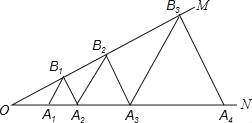
A. 32 B. 64 C. 128 D. 256
-
科目: 来源: 题型:
查看答案和解析>>【题目】九年级数学兴趣小组经过市场调查,得到某种图书每月的销售与售价的关系为函数关系如下表:
售价(元/本)
50
55
60
65
…
月销量(本)
2000
1800
1600
1400
…
已知该图书的进价为每本30元,设售价为x元.
(1)请用含x的式子表示:①销售该图书每本的利润是元,②月销量是件.(用x表示直接写出结果)
(2)若销售图书的月利润为48000元,则每本图书需要售价多少元?
(3)设销售该图书的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于P.弦CE平分∠ACB,交直径AB于点F,连结BE.
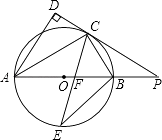
(1)求证:AC平分∠DAB;
(2)探究线段PC,PF之间的大小关系,并加以证明;
(3)若tan∠PCB= ,BE=
,BE= 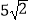 ,求PF的长.
,求PF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】同学们,足球是世界上第一大运动,你热爱足球运动吗?已知在足球比赛中,胜一场得3分,平一场得1分,负一场得0分,一队共踢了30场比赛,负了9场,共得47分,那么这个队胜了( )
A. 10场 B. 11场 C. 12场 D. 13场
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣x+3与x轴,y轴分别交于B,C两点,抛物线y=ax2+bx+c过A(1,0),B,C三点.
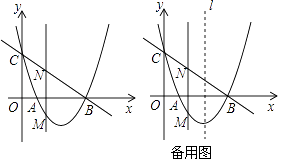
(1)求抛物线的解析式;
(2)若点M是抛物线在x轴下方图形上的动点,过点M作MN∥y轴交直线BC于点N,求线段MN的最大值.
(3)在(2)的条件下,当MN取得最大值时,在抛物线的对称轴l上是否存在点P,使△PBN是以BN为腰的等腰三角形?若存在,求出点P的坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数是( )

A. 400 B. 450 C. 500 D. 600
相关试题

