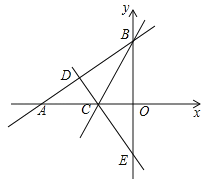
【题目】如图，在平面直角坐标系中，已知Rt△AOB的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，且OA、OB的长满足，∠ABO的平分线交x轴于点C过点C作AB的垂线，垂足为点D，交y轴于点E．

（1）求线段AB的长；

（2）求直线CE的解析式；

（3）若M是射线BC上的一个动点，在坐标平面内是否存在点P，使以A、B、M、P为顶点的四边形是矩形？若存在，请直接写出点P的坐标；若不存在，请说明理由．

参考答案：

【答案】（1）10；（2）；（3）存在，P（－3，10）或P（3，2）．

【解析】

试题分析：（1）根据非负数的性质，可求得OA和OB的长，然后根据勾股定理求得AB的长；

（2）证明△ACD∽△AOB，得到OC=CD，再根据△ACD∽△AOB，利用相似三角形的对应边的比相等求得OC的长，从而求得C的坐标，再由CD⊥AB，求得AB的解析式，即可求得CE的解析式；

（3）M是过A且垂直于AB的直线于BC的交点，首先求得M的坐标，然后分成四边形ABPM是矩形和APBM是矩形两种情况进行讨论．

试题解析：（1）∵，∴OA=8，OB=6，在直角△AOB中，AB===10；

（2）在△OBC和△DBC中，∵∠OBC=∠DBC，BC=BC，∠BOC=∠BDC，∴△OBC≌△DBC，∴OC=CD，设OC=x，则AC=8﹣x，CD=x．∵△ACD和△ABO中，∠CAD=∠BAO，∠ADC=∠AOB=90°，∴△ACD∽△AOB，∴，即，解得：x=3．即OC=3，则C的坐标是（﹣3，0）．设AB的解析式是，根据题意得：，解得：，则直线AB的解析式是，

设CD的解析式是，则，则，则直线CE的解析式是；

（3）设直线BC的解析式是，则：，解得：，则直线BC的解析式是；

设经过A且与AB垂直的直线的解析式是，则，解得：，

则过A且与AB垂直的直线的解析式是．

根据题意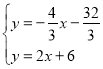得：，解得：，则M的坐标是（，）．

①当四边形ABPM是矩形时，线段AP的中点与线段BM的中点重合，设P（x，y），∵A（－8，0），B（0，6），M（，），则由中点坐标公式有：，，解得x=3，y=2，∴P（3，2）；

②当APBM是矩形时，线段AB的中点与线段PM的中点重合设P（x，y），∵A（－8，0），B（0，6），M（，），则由中点坐标公式有：，，解得x=－3，y=10，∴P（－3，10）．

综上所述，存在P（3，2）或P（－3，10）满足条件．

关闭