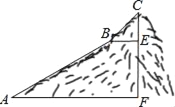
【题目】如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°.
(1)求AB段山坡的高度EF;
(2)求山峰的高度CF(结果保留根式).
参考答案:
【答案】(1) 400米;(2) (100![]() +400)米
+400)米
【解析】(1)作BH⊥AF于H,如图,在Rt△ABF中根据正弦的定义可计算出BH的长,从而得到EF的长;
(2)先在Rt△CBE中利用∠CBE的正弦计算出CE,然后计算CE和EF的和即可.
试题解析:(1)作BH⊥AF于H,如图,
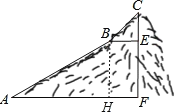
在Rt△ABH中,∵sin∠BAH=![]() ,
,
∴BH=800sin30°=400,
∴EF=BH=400米.
答:AB段山坡的高度EF为400米;
(2)在Rt△CBE中,∵sin∠CBE=![]() ,
,
∴CE=200sin45°=100![]() ,
,
∴CF=CE+EF=(100![]() +400)(米).
+400)(米).
答:山峰的高度CF为(100![]() +400)米.
+400)米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)比较大小:
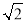 +1
+1 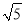 (填“>”、“<”或者“ =”)
(填“>”、“<”或者“ =”)(2)其实我们可以利用三角形的知识在方格纸上画图验证⑴的结果,请在图①中画出相应的图形(设小正方形的边长为1)

(3)请用(2)中的方法在图②中画图比较大小:
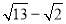
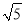
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一矩形纸片
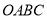 放在直角坐标系中,
放在直角坐标系中,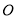 为原点,点
为原点,点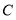 在
在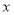 轴上,点
轴上,点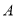 在
在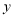 轴上,
轴上,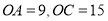 .
.(1)如图1,在
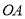 上取一点
上取一点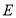 ,将
,将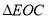 沿
沿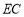 折叠,使
折叠,使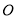 点落在
点落在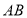 边上的
边上的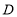 点处,求直线
点处,求直线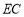 的解析式;
的解析式;(2)如图2,在
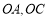 边上选取适当的点
边上选取适当的点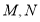 ,将
,将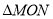 沿
沿 折叠,使
折叠,使 点落在
点落在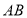 边上的点
边上的点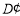 处,过
处,过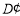 作
作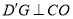 于点
于点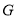 ,交
,交 于
于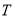 点,连接
点,连接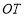 ,判断四边形
,判断四边形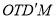 的形状,并说明理由;
的形状,并说明理由;(3)、在(2)的条件下,若点
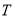 坐标
坐标 ,点
,点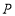 在
在 直线上,问坐标轴上是否存在点
直线上,问坐标轴上是否存在点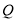 ,使以
,使以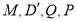 为顶点的四边形是平行四边形,若存在,请直接写出点
为顶点的四边形是平行四边形,若存在,请直接写出点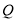 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.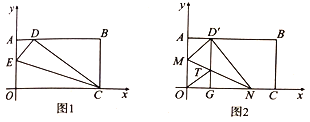
-
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆有单人间、双人间和三人间三种客房供游客租住,某旅行团有18人准备同时租用这三种客房共9间,且每个房间都住满,则租房方案共有______种.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC和△DBC都是边长为2的等边三角形.

(1)以图1中的某个点为旋转中心,旋转△DBC,就能使△DBC与△ABC重合,则满足题意的点为: (写出符合条件的所有点);
(2)将△DBC沿BC方向平移得到△D1B1C1,如图2、图3,则四边形ABD1C1是平行四边形吗?证明你的结论;
(3)在(2)的条件下,当BB1= 时,四边形ABD1C1为矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在
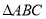 和
和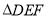 中,
中, ,
,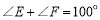 ,将
,将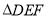 如图放置,使得
如图放置,使得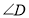 的两条边分别经过点
的两条边分别经过点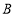 和点
和点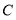 .
.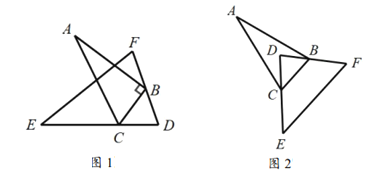
(1)当将
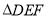 如图1摆放时,
如图1摆放时,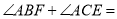 ______
______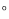 .
.(2)当将
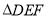 如图2摆放时,试问:
如图2摆放时,试问: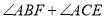 等于多少度?请说明理由.
等于多少度?请说明理由.(3)如图2,是否存在将
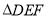 摆放到某个位置时,使得
摆放到某个位置时,使得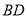 ,
,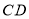 分别平分
分别平分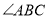 和
和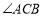 ?如果存在,请画出图形或说明理由.如果不存在,请改变题目中的一个已知条件,使之存在.
?如果存在,请画出图形或说明理由.如果不存在,请改变题目中的一个已知条件,使之存在. -
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为
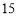 万元/辆,经销一段时间后发现:当该型号汽车售价定为
万元/辆,经销一段时间后发现:当该型号汽车售价定为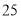 万元/辆时,平均每周售出
万元/辆时,平均每周售出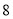 辆;售价每降低
辆;售价每降低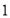 万元,平均每周多售出
万元,平均每周多售出 辆.
辆.(1)当售价为
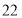 万元/辆时,平均每周的销售利润为___________万元;
万元/辆时,平均每周的销售利润为___________万元;(2)若该店计划平均每周的销售利润是
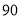 万元,为了尽快减少库存,求每辆汽车的售价.
万元,为了尽快减少库存,求每辆汽车的售价.
相关试题

