【题目】已知:线段AB=40cm.
(1)如图①,点P沿线段AB自点A向点B以3厘米/秒运动,同时点Q线段BA自B点向点A以5厘米/秒运动,问经过几秒后P、Q相遇?
(2)几秒钟后,P、Q相距16厘米?
(3)如图②,AO=PO=8厘米,∠POB=40°,点P绕点O以20度/秒的速度顺时针旋转一周停止,同时点Q沿直线BA自B点向点A运动,假若P、Q两点能相遇,求Q运动的速度.

参考答案:
【答案】(1)经过5秒钟后P、Q相遇;(2)经过3秒钟或7秒钟后,P、Q相距16cm;(3)点Q运动的速度为12cm/s或![]() cm/s.
cm/s.
【解析】
(1)根据相遇时,点P和点Q的运动的路程和等于AB的长列方程即可求解;
(2)设经过xs,P、Q两点相距10cm,分相遇前和相遇后两种情况建立方程求出其解即可;
(3)由于点P,Q只能在直线AB上相遇,而点P旋转到直线AB上的时间分两种情况,所以根据题意列出方程分别求解.
(1)设经过ts后,点P、Q相遇,
依题意,有3t+5t=40,
解得t=5.
答:经过5秒钟后P、Q相遇;
(2)设经过xs,P、Q两点相距16cm,由题意得
3x+5x+16=40或3x+5x16=40,
解得:x=3或x=7.
答:经过3秒钟或7秒钟后,P、Q相距16cm;
(3)点P,Q只能在直线AB上相遇,
则点P旋转到直线AB上的时间为40÷20=2s或(40+180)÷20=11s.
设点Q的速度为ycm/s,则有2y=4016,解得y=12或11y=40,解得![]()
答:点Q运动的速度为12cm/s或![]() cm/s.
cm/s.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别
成绩x分
频数
 人数
人数
第1组

6
第2组

8
第3组

14
第4组

a
第5组

10
请结合图表完成下列各题
 求表中a的值;
求表中a的值; 频数分布直方图补充完整;
频数分布直方图补充完整; 小亮想根据此直方图绘制一个扇形统计图,请你帮他算出成绩为
小亮想根据此直方图绘制一个扇形统计图,请你帮他算出成绩为 这一组所对应的扇形的圆心角的度数;
这一组所对应的扇形的圆心角的度数; 若测试成绩不低于80分为优秀,则本次测试的优秀率
若测试成绩不低于80分为优秀,则本次测试的优秀率 百分比
百分比 是多少?
是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】古运河是扬州的母亲河
 为打造古运河风光带,现有一段长为180米的河道整治任务由A、B两工程队先后接力完成
为打造古运河风光带,现有一段长为180米的河道整治任务由A、B两工程队先后接力完成 工程队每天整治12米,B工程队每天整治8米,共用时20天.
工程队每天整治12米,B工程队每天整治8米,共用时20天. 根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:
根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:甲:
 ;乙:
;乙:
根据甲、乙两名问学所列的方程组,请你分别指出未知数x、y表示的意义,然后在方框中补全甲、乙两名同学所列的方程组:
甲:x表示______,y表示______;
乙:x表示______,y表示______.
 求A、B两工程队分别整治河道多少米
求A、B两工程队分别整治河道多少米 写出完整的解答过程
写出完整的解答过程
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与直线y=
 x+2交于C、D两点,其中点C在y轴上,点D的坐标为(3,
x+2交于C、D两点,其中点C在y轴上,点D的坐标为(3,  ).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.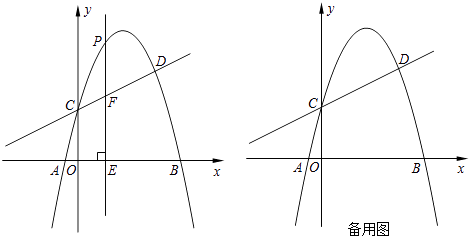
(1)求抛物线的解析式;
(2)若点P的横坐标为m,当m为何值时,以O、C、P、F为顶点的四边形是平行四边形?请说明理由.
(3)若存在点P,使∠PCF=45°,请直接写出相应的点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各数中,最小的数是( )
A.﹣2
B.﹣0.1
C.0
D.|﹣1| -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,AD切⊙O于点A,
 .则下列结论中不一定正确的是( )
.则下列结论中不一定正确的是( ) 
A.BA⊥DA
B.OC∥AE
C.∠COE=2∠CAE
D.OD⊥AC -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠CAB=50°.按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于点E、F;②分别以点E、F为圆心,大于
 EF的长为半径画弧,两弧相交于点G;③作射线AG交BC边于点D.则∠ADC的度数为 .
EF的长为半径画弧,两弧相交于点G;③作射线AG交BC边于点D.则∠ADC的度数为 . 
相关试题

