Question

【题目】如图，抛物线y=﹣x2+bx+c与直线y= x+2交于C、D两点，其中点C在y轴上，点D的坐标为（3， ）．点P是y轴右侧的抛物线上一动点，过点P作PE⊥x轴于点E，交CD于点F．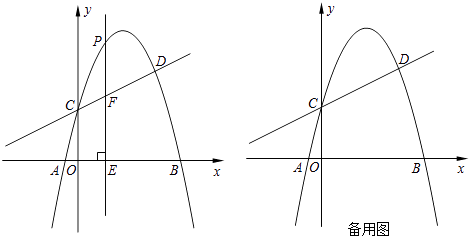

（1）求抛物线的解析式；
（2）若点P的横坐标为m，当m为何值时，以O、C、P、F为顶点的四边形是平行四边形？请说明理由．
（3）若存在点P，使∠PCF=45°，请直接写出相应的点P的坐标．

Answer 1

【答案】
（1）

解：在直线解析式y= x+2中，令x=0，得y=2，

∴C（0，2）．

∵点C（0，2）、D（3， ）在抛物线y=﹣x2+bx+c上，

∴ ，

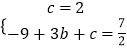解得b= ，c=2，

∴抛物线的解析式为：y=﹣x2+ x+2

（2）

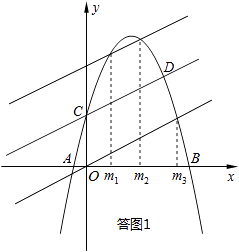
解：∵PF∥OC，且以O、C、P、F为顶点的四边形是平行四边形，

∴PF=OC=2，

∴将直线y= x+2沿y轴向上、下平移2个单位之后得到的直线，与抛物线y轴右侧的交点，即为所求之交点．

由答图1可以直观地看出，这样的交点有3个．

将直线y= x+2沿y轴向上平移2个单位，得到直线y= x+4，

联立 ，

解得x1=1，x2=2，

∴m1=1，m2=2；

将直线y= x+2沿y轴向下平移2个单位，得到直线y= x，

联立 ，

解得x3= ，x4= （在y轴左侧，不合题意，舍去），

∴m3= ．

∴当m为值为1，2或 时，以O、C、P、F为顶点的四边形是平行四边形

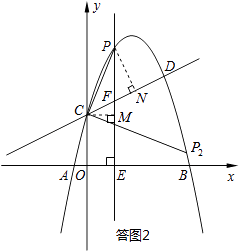
（3）

解：存在．

理由：设点P的横坐标为m，则P（m，﹣m2+ m+2），F（m， m+2）．

如答图2所示，过点C作CM⊥PE于点M，则CM=m，EM=2，

∴FM=yF﹣EM= m，

∴tan∠CFM=2．

在Rt△CFM中，由勾股定理得：CF= m．

过点P作PN⊥CD于点N，

则PN=FNtan∠PFN=FNtan∠CFM=2FN．

∵∠PCF=45°，

∴PN=CN，

而PN=2FN，

∴FN=CF= m，PN=2FN= m，

在Rt△PFN中，由勾股定理得：PF= = m．

∵PF=yP﹣yF=（﹣m2+ m+2）﹣（ m+2）=﹣m2+3m，

∴﹣m2+3m= m，

整理得：m2﹣ m=0，

解得m=0（舍去）或m= ，

∴P（ ， ）；

同理求得，另一点为P（ ， ）．

∴符合条件的点P的坐标为（ ， ）或（ ， ）．

【解析】（1）首先求出点C的坐标，然后利用待定系数法求出抛物线的解析式；（2）本问采用数形结合的数学思想求解．将直线y= x+2沿y轴向上或向下平移2个单位之后得到的直线，与抛物线y轴右侧的交点，即为所求之交点．由答图1可以直观地看出，这样的交点有3个．联立解析式解方程组，即可求出m的值；（3）本问符合条件的点P有2个，如答图2所示，注意不要漏解．在求点P坐标的时候，需要充分挖掘已知条件，构造直角三角形或相似三角形，解方程求出点P的坐标．