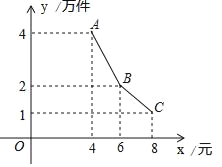
【题目】为了支持大学生创业,某市政府出台了一项优惠政策:提供10万元的无息创业贷款.小王利用这笔贷款,注册了一家淘宝网店,招收5名员工,销售一种火爆的电子产品,并约定用该网店经营的利润,逐月偿还这笔无息贷款.已知该产品的成本为每件4元,员工每人每月的工资为4千元,该网店还需每月支付其它费用1万元.该产品每月销售量y(万件)与销售单价x(元)万件之间的函数关系如图所示.
(1)求该网店每月利润w(万元)与销售单价x(元)之间的函数表达式;
(2)小王自网店开业起,最快在第几个月可还清10万元的无息贷款?
参考答案:
【答案】(1)当4≤x≤6时,w1=﹣x2+12x﹣35,当6≤x≤8时,w2=﹣![]() x2+7x﹣23;(2)最快在第7个月可还清10万元的无息贷款.
x2+7x﹣23;(2)最快在第7个月可还清10万元的无息贷款.
【解析】(1)y(万件)与销售单价x是分段函数,根据待定系数法分别求直线AB和BC的解析式,又分两种情况,根据利润=(售价﹣成本)×销售量﹣费用,得结论;
(2)分别计算两个利润的最大值,比较可得出利润的最大值,最后计算时间即可求解.
(1)设直线AB的解析式为:y=kx+b,
代入A(4,4),B(6,2)得:![]() ,
,
解得:![]() ,
,
∴直线AB的解析式为:y=﹣x+8,
同理代入B(6,2),C(8,1)可得直线BC的解析式为:y=﹣![]() x+5,
x+5,
∵工资及其他费作为:0.4×5+1=3万元,
∴当4≤x≤6时,w1=(x﹣4)(﹣x+8)﹣3=﹣x2+12x﹣35,
当6≤x≤8时,w2=(x﹣4)(﹣![]() x+5)﹣3=﹣
x+5)﹣3=﹣![]() x2+7x﹣23;
x2+7x﹣23;
(2)当4≤x≤6时,
w1=﹣x2+12x﹣35=﹣(x﹣6)2+1,
∴当x=6时,w1取最大值是1,
当6≤x≤8时,
w2=﹣![]() x2+7x﹣23=﹣
x2+7x﹣23=﹣![]() (x﹣7)2+
(x﹣7)2+![]() ,
,
当x=7时,w2取最大值是1.5,
∴![]() =
=![]() =6
=6![]() ,
,
即最快在第7个月可还清10万元的无息贷款.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某自动化车间计划生产480个零件,当生产任务完成一半时,停止生产进行自动化程序软件升级,用时20分钟,恢复生产后工作效率比原来提高了
 ,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件?
,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD(纸片)折叠,使点B与AD边上的点K重合,EG为折痕;点C与AD边上的点K重合,FH为折痕.已知∠1=67.5°,∠2=75°,EF=
 +1,求BC的长.
+1,求BC的长.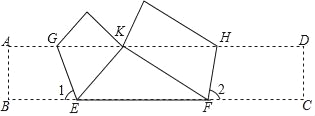
-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根调查结果绘制成的统计图(部分)如图所示.
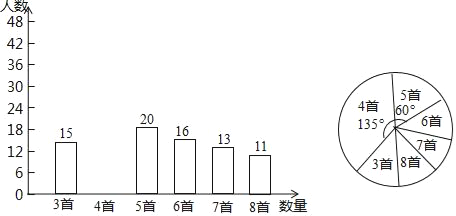
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表
一周诗词诵背数量
3首
4首
5首
6首
7首
8首
人数
10
10
15
40
25
20
请根据调查的信息
(1)活动启动之初学生“一周诗词诵背数量”的中位数为 ;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若把边长为1的正方形ABCD的四个角(阴影部分)剪掉,得四边形A1B1C1D1.试问怎样剪,才能使剩下的图形仍为正方形,且剩下图形的面积为原来正方形面积的
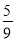 ?
?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)如图,矩形ABCD,AB=6cm,AD=2cm,点P以2cm/s的速度从顶点A出发沿折线A-B-C向点C运动,同时点Q以lcm/s的速度从顶点C出发向点D运动,当其中一个动点到达末端停止运动时,另一点也停止运动.
 (1)问两动点运动几秒,使四边形PBCQ的面积是矩形ABCD面积的
(1)问两动点运动几秒,使四边形PBCQ的面积是矩形ABCD面积的 ;
;(2)问两动点经过多长时间使得点P与点Q之间的距离为
 ?若存在,
?若存在,求出运动所需的时间;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在四边形BCDE中,BC⊥CD,DE⊥CD,AB⊥AE,垂足分别为C,D,A,BC≠AC,点M,N,F分别为AB,AE,BE的中点,连接MN,MF,NF.
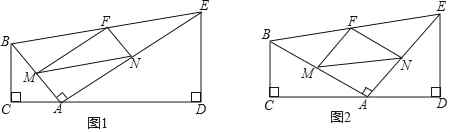
(1)如图②,当BC=4,DE=5,tan∠FMN=1时,求
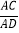 的值;
的值;(2)若tan∠FMN=
 ,BC=4,则可求出图中哪些线段的长?写出解答过程;
,BC=4,则可求出图中哪些线段的长?写出解答过程;(3)连接CM,DN,CF,DF.试证明△FMC与△DNF全等;
(4)在(3)的条件下,图中还有哪些其它的全等三角形?请直接写出.
相关试题

