【题目】下面的图表是我国数学家发明的“杨辉三角”,此图揭示了![]() (n为非负整数)的展开式的项数及各项系数的有关规律.请你观察,并根据此规律写出:
(n为非负整数)的展开式的项数及各项系数的有关规律.请你观察,并根据此规律写出:![]() _________.
_________.

参考答案:
【答案】a5-5a4b+10a3b2-10a2b3+5ab4-b5
【解析】
仿照![]() 的展开式的项数及各项系数的有关规律将
的展开式的项数及各项系数的有关规律将![]() 展开,即可得出
展开,即可得出![]() 的展开式.
的展开式.
解:由(1)“杨辉三角”可知:![]() 的第一项系数为1,第二项系数由上一层的相邻两数之和求得,……以此类推,
的第一项系数为1,第二项系数由上一层的相邻两数之和求得,……以此类推,
故![]() 展开式的各项系数如下图所示
展开式的各项系数如下图所示

根据右侧展开式可知:![]() 的展开式第一项a的指数为n,b的指数为0,第二项a的指数为n-1,b的指数为1,第三项a的指数为n-2,b的指数为2,……以此类推
的展开式第一项a的指数为n,b的指数为0,第二项a的指数为n-1,b的指数为1,第三项a的指数为n-2,b的指数为2,……以此类推
∴![]() = a5+5a4b+10a3b2+10a2b3+5ab4+b5
= a5+5a4b+10a3b2+10a2b3+5ab4+b5
∴![]() =
=![]() = a5+5a4(-b)+10a3(-b)2+10a2(-b)3+5a(-b)4+(-b)5
= a5+5a4(-b)+10a3(-b)2+10a2(-b)3+5a(-b)4+(-b)5
= a5-5a4b+10a3b2-10a2b3+5ab4-b5
故答案为:a5-5a4b+10a3b2-10a2b3+5ab4-b5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明家住房户型呈长方形,平面图如下(单位:米).现准备铺设整个长方形地面,其中三间卧室铺设木地板,其它区域铺设地砖.(房间内隔墙宽度忽略不计)

(1)求a的值;
(2)请用含x的代数式分别表示铺设地面需要木地板和地砖各多少平方米;
(3)按市场价格,木地板单价为300元/平方米,地砖单价为100元/平方米.装修公司有A,B两种活动方案,如表:
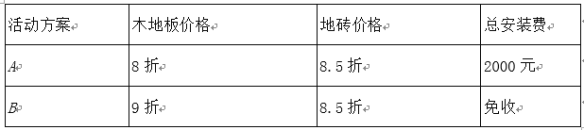
已知卧室2的面积为21平方米,则小方家应选择哪种活动,使铺设地面总费用(含材料费及安装费)更低?
-
科目: 来源: 题型:
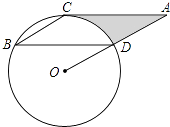
查看答案和解析>>【题目】如图,点B,C,D都在⊙O上,过C点作CA∥BD交OD的延长线于点A,连接BC,∠B=∠A=30°,BD=2
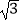 .
.
(1)求证:AC是⊙O的切线;
(2)求由线段AC、AD与弧CD所围成的阴影部分的面积.(结果保留π) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(-2,-6),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
(1)求证:△ABC≌△DCB;
(2)△OBC是何种三角形?证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,M是△ABC的边BC的中点,AN平分
 ,BN
,BN AN于点N,延长BN交AC于点D,已知AB=10,AC=16.
AN于点N,延长BN交AC于点D,已知AB=10,AC=16.
(1)求证:BN=DN;
(2)求MN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,把矩形OCBA绕点C顺时针旋转α角,得到矩形FCDE,设FC与AB交于点H,且A(0,4),C(6,0).
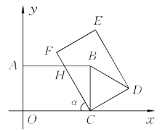
(1)当α=45°时,求H点的坐标.
(2)当α=60°时,ΔCBD是什么特殊的三角形?说明理由.
(3)当AH=HC时,求直线HC的解析式.
相关试题

