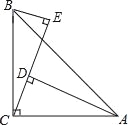
【题目】如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.
(1)证明:△BCE≌△CAD;
(2)若AD=25cm,BE=8cm,求DE的长.
参考答案:
【答案】(1)证明见解析;(2)DE=17cm.
【解析】试题分析:(1)根据垂直的定义可得∠ADC=∠E=90°,然后根据同角的余角相等求出∠CBE=∠ACD,再利用“角角边”证明△BCE和△CAD全等;
(2)根据全等三角形对应边相等,通过线段的和差即可求得.
试题解析:(1)∵∠ACB=90°,BE⊥CE,AD⊥CE,
∴∠BEC=∠ACB=∠ADC=90°,
∴∠ACE+∠BCE=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,
在△BCE和△CAD中, 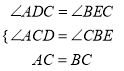 ,
,
∴△BCE≌△CAD;
(2)∵△BCE≌△CAD,
∴AD=CE,BE=CD,
∴DE=CE﹣CD=AD﹣BE=25﹣8=17(cm).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若正比例函数y=kx的图象经过点(1,2),则k=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】五边形的外角和为( )
A.360°B.540°C.720°D.900°
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“全等三角形对应边上的高线相等”的已知是________,结论是________.
-
科目: 来源: 题型:
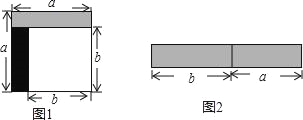
查看答案和解析>>【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是 ;(请选择正确的一个)
A、a2﹣2ab+b2=(a﹣b)2
B、a2﹣b2=(a+b)(a﹣b)
C、a2+ab=a(a+b)
(2)应用你从(1)选出的等式,完成下列各题:
①已知x2﹣4y2=12,x+2y=4,求x﹣2y的值.
②计算:(1﹣
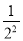 )(1﹣
)(1﹣ )(1﹣
)(1﹣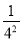 )…(1﹣
)…(1﹣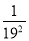 )(1﹣
)(1﹣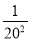 ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系内一点P(2,3)关于原点对称的点的坐标是( )
A. (2,﹣3) B. (2,3) C. (﹣2,3) D. (﹣2,﹣3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出两个三视图形状都一样的几何体:__________、__________.
相关试题

